Work It Out Chapter 9(24)

Question 1 of 3

Work It Out

true

You must read each slide, and complete any questions on the slide, in sequence.

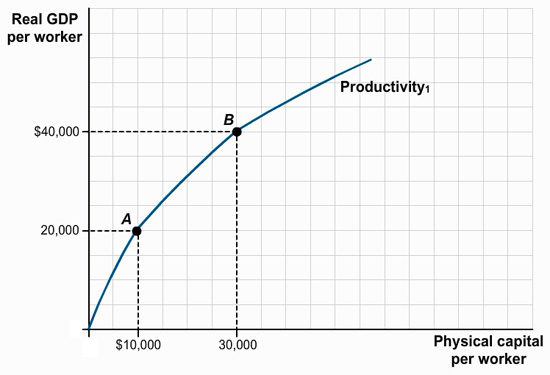
You are hired as an economic consultant to the countries of Albernia and Brittania. Each country’s current relationship between physical capital per worker and output per worker is given by the curve labeled “Productivity₁” in the accompanying diagram. Albernia is at point A and Brittania is at point B.

The graph shows the Productivity curve that originates at the intersection of the horizontal and vertical axes. The horizontal axis is labeled ‘Physical capital per worker’. The vertical axis is labeled ‘Real GDP per worker’. There are two points, A and B, indicated on the productivity curve. Point A corresponds to a value of 10,000 dollars on the horizontal axis and 20,000 dollars on the vertical axis. Point B corresponds to a value of 30,000 dollars on the horizontal axis and 40,000 dollars on the vertical axis.

In the relationship depicted by the curve Productivity₁, which of the following statements are true regarding the relationship between physical capital per worker and real GDP per capital for both countries?

These countries experience increasing returns to physical capital per worker with technology and human capital per worker being fixed.

These countries experience diminishing returns to physical capital per worker with technology and physical capital per worker being fixed.

These countries experience diminishing returns to physical capital per worker with technology and human capital per worker being fixed.

These countries experience increasing returns to physical capital per worker with physical and human capital per worker being fixed.

0:49

WIO_Krugman_Chapter24_01

Video Player is loading.

Current Time 0:00

Duration 0:00

Loaded: 0%

Stream Type LIVE

Remaining Time 0:00

Assuming that the amount of human capital per worker and the technology are held fixed in each country, can you recommend a policy to generate a doubling of real GDP per capita in Albernia from $20,000 to $40,000?

Albernia should increase its physical capital per worker to $30,000.

Albernia should increase its level of labor.

Albernia should increase its human capital per worker to $30,000.

Albernia should increase its physical capital per worker to $20,000.

0:37

WIO_Krugman_Chapter24_02

Video Player is loading.

Current Time 0:00

Duration 0:00

Loaded: 0%

Stream Type LIVE

Remaining Time 0:00

Assume that an increase in human capital doubles the output per worker when physical capital per worker equals $10,000. Using the graph below identify the point on the either Productivity₁ or Productivity₂ for Albernia.

The graph shows two Productivity curves (Productivity 1 and Productivity 2) that originate at the intersection of the horizontal and vertical axes. The horizontal axis is labeled ‘Physical capital per worker’. The vertical axis is labeled ‘Real GDP per worker’. There are two points, A and B, indicated on Productivity 1. Point A corresponds to a value of 10,000 dollars on the horizontal axis and 20,000 dollars on the vertical axis. Point B corresponds to a value of 30,000 dollars on the horizontal axis and 40,000 dollars on the vertical axis. Point C is indicated on the second productivity curve (Productivity 2) and corresponds to a value of 10,000 dollars on the horizontal axis and 40,000 dollars on the vertical axis. The space between the two curves is indicated by a vertical arrow.

Point B

Point A

Point C

0:27

WIO_Krugman_Chapter24_03

Video Player is loading.

Current Time 0:00

Duration 0:00

Loaded: 0%

Stream Type LIVE

Remaining Time 0:00

Work It OutChapter 9(24)

Question 1 of 3

Step 1

Step 2

Step 3