Chapter 1. Chapter 6
Step 1
Work It Out
true
true
You must read each slide, and complete any questions on the slide, in sequence.
Question
The accompanying table shows a car manufacturer’s total cost of producing cars.
| Quantity of Cars | TC |
|---|---|
| 0 | $500,000 |
| 1 | 540,000 |
| 2 | 560,000 |
| 3 | 570,000 |
| 4 | 590,000 |
| 5 | 620,000 |
| 6 | 660,000 |
| 7 | 720,000 |
| 8 | 800,000 |
| 9 | 920,000 |
| 10 | 1,100,000 |
Table
What is this manufacturer’s fixed cost?
Fixed cost: $ydrliJ5SZDWEX5Ybh7R7VkGiPdLrvnvttW1qLWexdVYtIAR7
Correct! For further review see section “From the Production Function to Cost Curves.”
Incorrect, recall that the firm incurs a fixed cost even when production is zero. When the quantity of cars is zero, the total cost will equal the fixed cost. Using the table above this means the fixed cost is $500,000. For further review see section “From the Production Function to Cost Curves.”
What is this manufacturer’s fixed cost?
0:23
Step 2
Question
Complete the table by calculating the variable cost (VC) for each level of output.
| Quantity of Cars | TC | Variable Cost (VC) |
|---|---|---|
| 0 | $500,000 | $ZGVg74NXfao7Qvv4pKuELJf1skw= |
| 1 | 540,000 | $opBM8ulVoC7fTDhhsIy3qg== |
| 2 | 560,000 | $sEFP+60ak/FM7ljc248Etg== |
| 3 | 570,000 | $rKizAeaKSUJDuoP3JikH4g== |
| 4 | 590,000 | $tDd4MaezKuGlGQwjVcxL1A== |
| 5 | 620,000 | $eoKjWDAmVFKoWi6DmT4M7F+RMek= |
| 6 | 660,000 | $FFh2Qx7t9MUxV+5rPNmLuIzBLXs= |
| 7 | 720,000 | $gtQXE97KJSodee8uC3cIdMVRTtk= |
| 8 | 800,000 | $JrivKM8JRXCI7HHZ//PBpLlWor8= |
| 9 | 920,000 | $xncpv07PCGz7CrsFby2DaZ69Pj4= |
| 10 | 1,100,000 | $/uuRs3rQCGKTKUw5xSwt/+FKYnI= |
Table
Recall that the variable cost is the difference between total cost and fixed cost. In part A you found fixed costs were $500,000. This is also the level of total cost when output is zero. To find variable cost subtract $500,000 from total cost for each level of output. For example, when the company produces 5 cars, variable costs are $620,000 - $500,000 = $120,000. For further review see section “From the Production Function to Cost Curves.”
Complete the table by calculating the variable cost (VC) for each level of output.
0:46
Step 3
Question
Complete the table: for each level of output except zero output, calculate the average variable cost (AVC), average total cost (ATC), and average fixed cost (AFC) (please round your answer to the nearest whole number).
| Quantity of Cars | TC | Variable Cost (VC) | Average variable cost (AVC) | Average total cost (ATC) | Average fixed costs (AFC) |
|---|---|---|---|---|---|
| 0 | $500,000 | 0 | - | - | - |
| 1 | $540,000 | 40,000 | {{40000_40,000}} | {{540000_540,000}} | {{500000_500,000}} |
| 2 | 560,000 | 60,000 | {{30000_30,000}} | {{280000_280,000}} | {{250000_250,000}} |
| 3 | 570,000 | 70,000 | {{23333_23,333}} | {{190000_190,000}} | {{166667_166,667}} |
| 4 | 590,000 | 90,000 | {{22500_22,500}} | {{147500_147,500}} | {{125000_125,000}} |
| 5 | 620,000 | 120,000 | {{24000_24,000}} | {{124000_124,000}} | {{100000_100,000}} |
| 6 | 660,000 | 160,000 | {{26667_26,667}} | {{110000_110,000}} | {{83333_83,333}} |
| 7 | 720,000 | 220,000 | {{31429_31,429}} | {{102857_102,857}} | {{71429_71,429}} |
| 8 | 800,000 | 300,000 | {{37500_37,500}} | {{100000_100,000}} | {{62500_62,500}} |
| 9 | 920,000 | 420,000 | {{46667_46,667}} | {{102222_102,222}} | {{55556_55,556}} |
| 10 | 1,100,000 | 600,000 | {{60000_60,000}} | {{110000_110,000}} | {{50000_50,000}} |
Table
Average variable cost is VC/Q, for example the AVC for 4 cars is $90,000/4 = $22,500. Average total cost is TC/Q, for example the ATC for 6 cars is $660,000/6 = $110,000. Average fixed cost is FC/Q. Remember fixed costs are $500,000. For 5 cars AFC are $500,000/5 = $100,000. You should make notice that AFC are always decreasing as quantity increases. For further review see section “Two Key Concepts: Marginal Cost and Average Cost.”
2:14
Step 4
Question
Complete the table by calculating the marginal cost (VC) for each level of output.
| Quantity of Cars | TC | Marginal Cost (MC) |
|---|---|---|
| 0 | $500,000 | - |
| 1 | 540,000 | opBM8ulVoC7fTDhhsIy3qg== |
| 2 | 560,000 | EVnPUUahpF4ASTkz/J+qmw== |
| 3 | 570,000 | FPVg3kT8sXb07noVdPTKDw== |
| 4 | 590,000 | EVnPUUahpF4ASTkz/J+qmw== |
| 5 | 620,000 | YWX2v9hCFftqkavFIrX9YA== |
| 6 | 660,000 | opBM8ulVoC7fTDhhsIy3qg== |
| 7 | 720,000 | sEFP+60ak/FM7ljc248Etg== |
| 8 | 800,000 | UtTrhUsxAbWlHreXCQAjLg== |
| 9 | 920,000 | eoKjWDAmVFKoWi6DmT4M7F+RMek= |
| 10 | 1,100,000 | n/hOgAdSPHFPQ1nqL5y1joZTDEc= |
Table
Recall that marginal cost is change in total cost divided by the change in quantity (MC = ΔTC/ΔQ). In this problem the change in quantity is always one which implies marginal cost will be the difference in total cost as output increases by one unit. For example, as output increases from 1 to 2 cars, total costs increase from $540,000 to $560,000. The change in total costs are $20,000 which is also the marginal cost. For further review see section “Two Key Concepts: Marginal Cost and Average Cost.”
Complete the table by calculating the marginal cost (VC) for each level of output.
1:09
Step 5
Question
Label the manufacturer’s AVC, ATC, and MC curves.
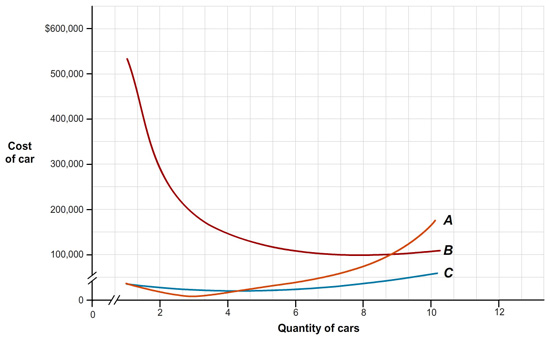
Curve A is wBBitpIsTMrmnpnp1XTC5JlSNjc=
Curve B is sbyrXt3yS9c4DsjBkFygX54qr8Q=
Curve C is MMi0syRscQaH9XZIYtYyjHKnQkQ=
Looking at the tables previously, it is fairly easy to see that ATC is significantly larger than MC and AVC at low levels of output. MC cost will always intersect ATC and AVC at each lines minimum point. Finally, AVC will always lie below ATC. Remember that ATC = AFC + AVC. As output increases ATC and AVC will approach each other as AFC continues to decrease. . For further review see section “Two Key Concepts: Marginal Cost and Average Cost.”
Label the manufacturer’s AVC, ATC, and MC curves.
0:55