TABLE OF CONTENTS

Question 1 of 3

Work It Out
true
true
You must read each slide, and complete any questions on the slide, in sequence.

You are hired as an economic consultant to the countries of Albernia and Brittania. Each country’s current relationship between physical capital per worker and output per worker is given by the curve labeled “Productivity1” in the accompanying diagram. Albernia is at point A and Brittania is at point B.

The graph shows the Productivity curve that originates at the intersection of the horizontal and vertical axes. The horizontal axis is labeled ‘Physical capital per worker’. The vertical axis is labeled ‘Real GDP per worker’. There are two points, A and B, indicated on the productivity curve. Point A corresponds to a value of 10,000 dollars on the horizontal axis and 20,000 dollars on the vertical axis. Point B corresponds to a value of 30,000 dollars on the horizontal axis and 40,000 dollars on the vertical axis.

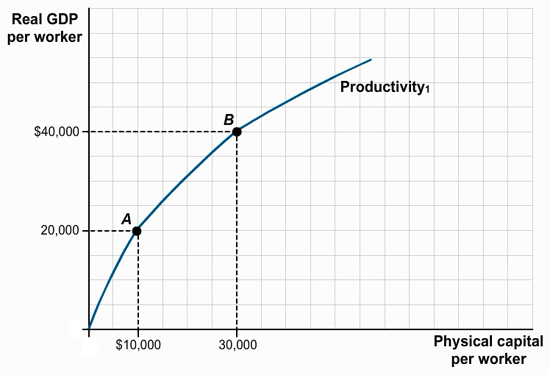
In the relationship depicted by the curve Productivity1, which of the following statements are true regarding the relationship between physical capital per worker and real GDP per capital for both countries?
0:49
WIO_Krugman_Chapter24_01
Current Time 0:00
Duration 0:00
Loaded: 0%
Stream Type LIVE
Remaining Time 0:00
 
1x
    • Chapters
    • descriptions off, selected

      Assuming that the amount of human capital per worker and the technology are held fixed in each country, can you recommend a policy to generate a doubling of real GDP per capita in Albernia from $20,000 to $40,000?

      The graph shows the Productivity curve that originates at the intersection of the horizontal and vertical axes. The horizontal axis is labeled ‘Physical capital per worker’. The vertical axis is labeled ‘Real GDP per worker’. There are two points, A and B, indicated on the productivity curve. Point A corresponds to a value of 10,000 dollars on the horizontal axis and 20,000 dollars on the vertical axis. Point B corresponds to a value of 30,000 dollars on the horizontal axis and 40,000 dollars on the vertical axis.
      0:37
      WIO_Krugman_Chapter24_02
      Current Time 0:00
      Duration 0:00
      Loaded: 0%
      Stream Type LIVE
      Remaining Time 0:00
       
      1x
        • Chapters
        • descriptions off, selected

          Assume that an increase in human capital doubles the output per worker when physical capital per worker equals $10,000. Using the graph below identify the point on the either Productivity1 or Productivity2 for Albernia.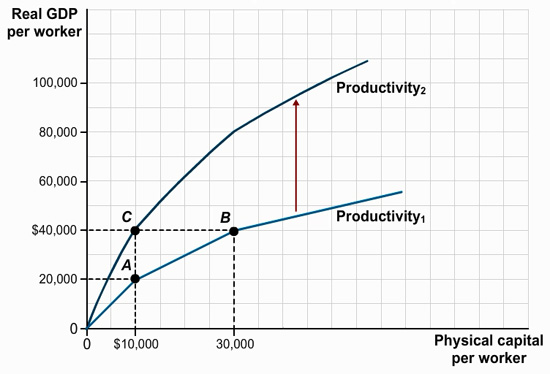

          The graph shows two Productivity curves (Productivity 1 and Productivity 2) that originate at the intersection of the horizontal and vertical axes. The horizontal axis is labeled ‘Physical capital per worker’. The vertical axis is labeled ‘Real GDP per worker’. There are two points, A and B, indicated on Productivity 1. Point A corresponds to a value of 10,000 dollars on the horizontal axis and 20,000 dollars on the vertical axis. Point B corresponds to a value of 30,000 dollars on the horizontal axis and 40,000 dollars on the vertical axis. Point C is indicated on the second productivity curve (Productivity 2) and corresponds to a value of 10,000 dollars on the horizontal axis and 40,000 dollars on the vertical axis. The space between the two curves is indicated by a vertical arrow.
          0:27
          WIO_Krugman_Chapter24_03
          Current Time 0:00
          Duration 0:00
          Loaded: 0%
          Stream Type LIVE
          Remaining Time 0:00
           
          1x
            • Chapters
            • descriptions off, selected