Question 1 of 3
Step 1
Country A and country B both have the production function
Y = F(K, L) = K1/2L1/2.
Does this production function have constant returns to scale?
What is the per‑worker production function, y = f(k)?
The per-worker production function is _______.
Step 2
Country A and country B both have the production function
Y = F(K, L) = K1/2L1/2.
Assume that neither country experiences population growth or technological progress and that 5 percent of capital depreciates each year. Assume further that country A saves 10 percent of output each year and country B saves 20 percent of output each year. Using your answer from part (b) and the steady state condition that investment equals depreciation, find the steady state level of capital per worker for each country. Then find the steady state levels of income per worker and consumption per worker.
Country A:
k* =
y* =
c* =
Country B:
k* =
y* =
c* =

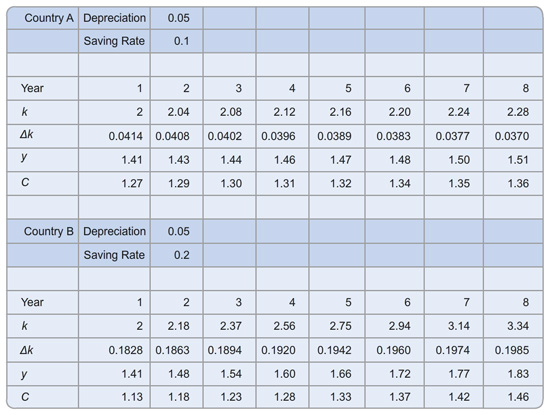
Step 3
Country A and country B both have the production function
Y = F(K, L) = K1/2L1/2.
Suppose that both countries start off with a capital stock per worker of 2. What are the levels of income per worker and consumption per worker? Round your answers to two decimal places.
Country A:
y =
c =
Country B:
y =
c =