Chapter 2. EVOLUTION I—POPULATION GENETICS

Learning Objectives

Pre-Lab—Hardy-Weinberg
false
false

General Purpose

Conceptual

  • Define evolution as it is defined by biologists and be able to describe how the components relate to experiments testing the concept of evolution.
  • Define the term gene pool and explain how it relates to the concept of evolution.
  • Gain an understanding of the concept of genetic equilibrium and the conditions required for it to occur.
  • Gain an understanding of the relationship between genetic equilibrium and evolution.
  • Gain an understanding of the Hardy-Weinberg equation and how it relates to population evolution.
  • Gain an understanding of the impact of selection, mutation, and population size.

Procedural

  • Be able to use the Hardy-Weinberg equation to calculate allele frequencies.
  • Be able to graph the data obtained in this experiment, including a figure legend, and be able to describe any trends in the data.

General Purpose

This lab will help familiarize you with some of the aspects of the theory of evolution. The theory of evolution is the one central theme that runs throughout the life sciences. While a complete understanding of this theory cannot be obtained in a few laboratory exercises, many of the crucial components can be explored. The laboratory exercises described here focus on how alleles are distributed in populations, what impacts the frequencies of alleles, how selection can change the resulting populations, and how mutation might influence the process of selection.

General Background Information

The theory of evolution emphasizes that populations, not individuals, evolve. A population consists of all the members of the same species that live in one location. Each member of a population is assumed to be free to reproduce with any other member, and when reproduction occurs, the genes of one generation are passed on following Mendelian inheritance principles. In a population of sexually reproducing individuals, the various alleles of all the genes in all the individuals make up a gene pool for the population. The gene pool of a population can be described in terms of allele frequencies.

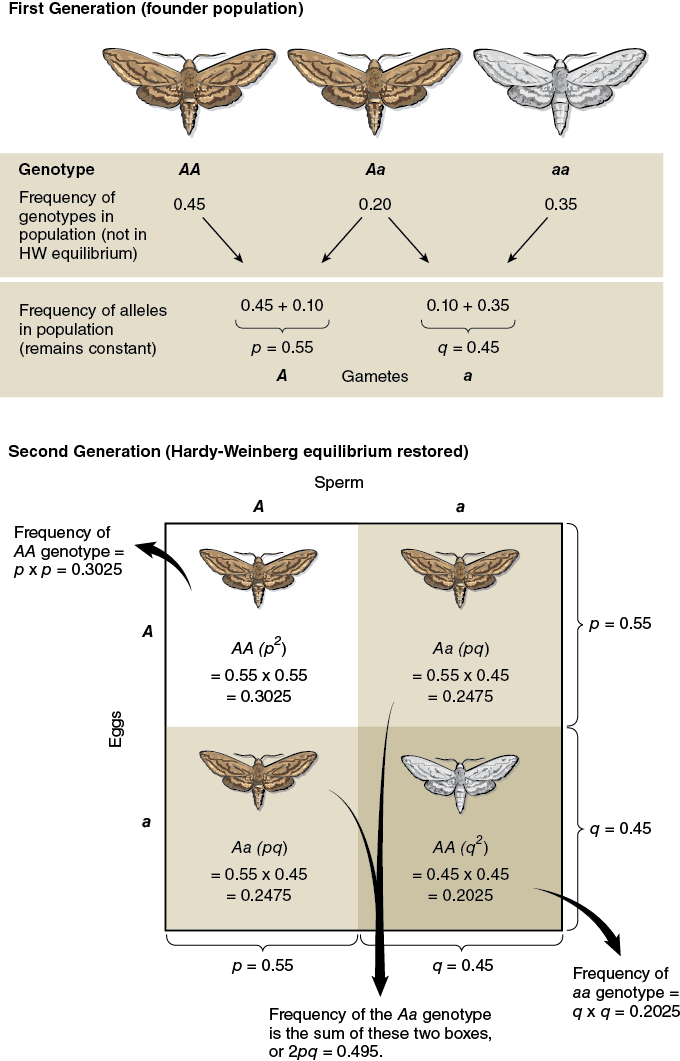
Two independent investigators, G.H. Hardy and W. Weinberg, realized that the binomial equation

p2 + 2pq + q2 = 1

could be used to directly calculate the genotype frequencies of a population in which there were only two alleles for a particular gene. This equation has been termed the “Hardy-Weinberg equation.”

Assume that in any generation for a population, each type of sperm had an equal chance to fertilize each type of egg. Assign the letter “p” to the dominant allele (A) and the letter “q” to the recessive allele (a); then

In this case

p2 = the frequency of homozygous dominant individuals (AA)

q2 = the frequency of homozygous recessive individuals (aa)

2pq = the frequency of heterozygous individuals (Aa)

To use this equation to calculate the genotypic frequencies in a population, it is necessary to know the frequencies of each allele. For example, suppose the dominant allele (p) has a frequency of 0.7 and the recessive allele (q) has a frequency of 0.3, then the genotype frequencies of the population would be:

p2 (homozygous dominant) = 0.7 × 0.7 = 0.49

q2 (homozygous recessive) = 0.3 × 0.3 = 0.09

2pq (heterozygous) = 2 × (0.7 × 0.3) = 0.42

Note that these genoptype frequencies sum to 1.00.

The frequencies of the two alleles (p and q) must also sum to 1.00.

Figure 1-1. This shows the relationships between the Mendalian terms homozygous dominant, homozygous recessive, and heterozygous to the variables in the Hardy-Weinberg equation.

If you know the percentage of individuals in a population that shows the recessive phenotype, it is possible to calculate the genotype frequencies and the allele frequencies. Suppose, by inspection, you determine 16% of the human population has a continuous hairline (recessive phenotype). This means that 84% of humans must have a widow’s peak. Using the Hardy-Weinberg equation, you can determine how many individuals are homozygous dominant and how many are heterozygous.

First, convert 16% to a decimal or frequency (0.16).

0.16 = q2 and therefore q = 0.4. Since p + q = 1.0, then p = 0.6.

Once values for p and q are known, then you can plug them into the Hardy-Weinberg equation and determine

p2 (homozygous dominant) = 0.36 or 36%

2pq (heterozygous) = 0.48 or 48%

q2 (homozygous recessive) = 0.16 or 16%

The Hardy-Weinberg equation can be used to calculate the genotype frequencies of a pair of alleles at a gene locus in an established population. It can also be used to predict genotype frequencies of the next generation as long as there have been no changes in the gene pool. When there have been no changes, then genetic equilibrium occurs and the population does not evolve with respect to those alleles.

Genetic equilibrium will only occur when

  1. The population is large enough to be unaffected by random gene changes.
  2. There is no gene flow (immigration or emigration).
  3. There are no mutations occurring or there is mutational equilibrium.
  4. There is random mating.
  5. There is no natural selection.

All of these conditions must be met for a population to be in genetic equilibrium. In natural populations all of these conditions are almost never met.

Click to view Hardy article.

Pre-Lab Quiz

Proceed to the Pre-Lab Quiz