Chapter 1. WIO_Krugman_Chapter6
Step 1
Work It Out
true
true
You must read each slide, and complete any questions on the slide, in sequence.
Question
Nile.com, the online bookseller, wants to increase its total revenue. One strategy is to offer a 10% discount on every book it sells. Nile.com knows that its customers can be divided into two distinct groups according to their likely responses to the discount. The accompanying table shows how the two groups respond to the discount.
| Group A (sales per week) | Group B (sales per week) 1 | |
|---|---|---|
| Volume of sales before the 10% discount | 1.55 million | 1.50 million |
| Volume of sales after the 10% discount | 1.65 million | 1.70 million |
Table
Using the midpoint method, calculate the price elasticity of demand for group A and B in the table.
Group A:XUDQwJci5iCNZdnH
Group B:y8Sz/PJSTJs=
3
Using the midpoint method, the percent change in the quantity demanded by group A is
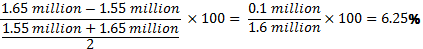 And since the change in price is 10%, the price elasticity of demand for group A is
(%∆Q)/(%∆P)=(6.25%)/(10%)=0.625
Next we need to use the midpoint method to find the percent change in the quantity demanded by group B:
(1.7 million-1.5 million)/((1.7 million+1.5 million)/2) ×100= (0.2 million)/(1.6 million)×100=12.5%
And since the change in price is 10%, the price elasticity of demand for group B is
(%∆Q)/(%∆P)=(12.5%)/(10%)=1.25
For further review see section “An Alternative Way to Calculate Elasticities: The Midpoint Method” (link to section in ebook).
And since the change in price is 10%, the price elasticity of demand for group A is
(%∆Q)/(%∆P)=(6.25%)/(10%)=0.625
Next we need to use the midpoint method to find the percent change in the quantity demanded by group B:
(1.7 million-1.5 million)/((1.7 million+1.5 million)/2) ×100= (0.2 million)/(1.6 million)×100=12.5%
And since the change in price is 10%, the price elasticity of demand for group B is
(%∆Q)/(%∆P)=(12.5%)/(10%)=1.25
For further review see section “An Alternative Way to Calculate Elasticities: The Midpoint Method” (link to section in ebook).
0:10

Step 2
Question
| Group A (sales per week) | Group B (sales per week) | |
|---|---|---|
| Volume of sales before the 10% discount | 1.55 million | 1.50 million |
| Volume of sales after the 10% discount | 1.65 million | 1.70 million |
Table
3
0:10

Step 3
Question
3+KNUgCtTB7zpSatqMQb6+Fi9+/rLG5mXDkcW03OM7M9yWXNw7vwNmB9Sas1zEWCJkK541XWLCKMx5hMNtS36u3ACMGUEDXplM+V15VIMArg2W30SL1Le8o6cG58NONqPN8HymUjiCO8KyE6b+jcs1fGY0LQ1tLkrLmwHwWdHC1p2AUZGKPkHncSUh7Xp9T62fbIYwYaqG4qI1r2fScSUo/8MmMHkDTDx8APaHu4Kc1tNIDVwhiULYE3WwopK9wC5/iIV+tODqiPiYoVlIvJwdPq81UruSIUKSgwcctbQbzP3x7V0BNX3+4RAr4p8Ma7978Q+dZ78rUliptAQW7HAZyGWonQfqwHHfxgLeicgSunNEqzBIjlEzf4FTVbOHYojNPvBP55b+rrLDOujMOjc485InPEO8TW6sm22so0Oe7CZxmCfQ6q0jxbQsD3O10k3QEN4cceDvqwYBOEIhBOSqYllfJdOjyP5w5zJiA14OOF85IMLYpK5Snn8rsUIFXZM3gLG4szGrtT/RT7H/5cxB5mEyomkiLj+cZoPsj55u9USwYX/gSlVo0VXw5VLrj95f0Ncp7YOqy5ugnGpuIp9t+/z6BnCTsLgLPNF9vG60hTkJebX/ZVS166MqUma8ylCOxPaYfLalJZLuHkQc5adiSNSXjI5qZkxkyHnoQS+asfX0GrS6vAZ3f0DJkJWzvzSUZgpJVh4bQQlyEhw5yWeb1KrR4E5opBsiTrWu+J9PHYHKB8Xcr1p713GhiYJctFNEJiO2tGgmv8zIM4qSLhnFybEk11/weVhVN/aEzBkZupdB3bEHnVbA4oxUjXWWFTD/NuTmc5vq8axeJfCsFZjdQI4MHyvkV4JorFYCA0XrzTPvwbm/UBvUd0n6LtwRyn/g3OD7V88fy5atgJB0DwRt0X5BmUDruXhPW+ou2Jul7shh0/ARU2dUoPd73oPZ+vLY/TFbWF8AVFAdKLQZ3EJYji5bIMYxEf5hqlmpz1pvf6ItSL7ZYPnFV2Y8yAsfTuFH9kEE32+CQD69HfH8Bh21XQZ6WHCpDl2gQzJN9rL1G3cQpQLjvu9En28qnfShzNajnho47hE/JUON10e/pRE7YC/nzE0SUOPjcCxHJz5lidWkj9xvpQYxCqXNxc5E9gZ2scg3dwKXQFdWAGVi4mK/ZrQR7EipaOEl7tJgO/TlclgW/SdpPdne21bQDh1PkTrM10F0mMJPbl7eGlHiZYFwCl5aS46MVOgI/xeB8ZrL1sBxk6U2msheVZcU9+xeN9VayYU68ZDq0u8rmFIj2yXEALZg4IPVORjukjQPt+oHSANHZmQB2npWc76BjgbUXT8u/2yDC0OkjNYW9NOoBZqB0sgy8LLucfEb6q9abTpSDJvgGyklBYIrFpMYXS9PnzBGtza6fC8qbB7u1L6ckRj0i7H+ok9+s+WQGlJGjGRQq/o8HPL6Szrg7WYCDOBtsBb1uWa8K1DI0vv8WWhFdlv+J09CwbfA3yKvEJTF9UjUAPy1cIvPRnG0jRwg19JRZ1vhEAHUNfI0hq/FTIupNycdzLl/a5GsMB+/dNZkg4UWUijQpQKohNvXfPzC3GCJpTjViA6biC7iulHp/LY65AbZmHbt5KxxHwzacKF7ZBqc3oEK3/JfYbH1eWk72i6jayIMmVJtsJtP6gG6CqBFaUJiXYVn+t+zyarQ3o+mIqTm5ciEK7xpcQ6VFFbyTJWE6m2+JJabo5ik7xQJBK+9AwSjYRrOfGgNCW19+U6nxEoGDGXflUE+SfdpJHoUtyK6NSMl2/kc4uX8RvB51dAwR7yfYm6L51XHk5DU0a2+vn3MaxOUXKiErcMhoaJhhwGKu1jetnk7oOZwkj2ijhEKG2FDv6YnhRDqLKEW+L2fAiIhVznz/xFWy9qzXR2TrqJL9p2Xj0UFt/ORqjvTx04ll2I4jrFQPfJqzIUsACTFDuDoW+UtVcqijJc7J2CR634D4Ddu0q02KTnWktoih9ps2xVrre8SnE341sQXai18jNEI93DyAID3+gK8bT9WsIEH6ynpLxW3UU3HK6IxIPtBb3XWh0O96eU/M6YcgD5yieLX5eb4j/lhamNADs4vM/bYxhJLbO4ek5ZOP80tfIVmKP2LZUyfmuc7gGX0tVv1JqC0umV8y+2ZsDQ2mBzJ4V7OSMYc+uuzzm7wAIoWxvQUHDkw==3
0:10
