Chapter 1. Experiment 10
Vapor Pressure & Colligative Properties
Purpose of the Experiment
To determine the vapor pressure of a pure volatile solvent and investigate how the colligative properties of a solution affect the vapor pressure of the solvent.
Background Required
This experiment will use basic laboratory techniques using both a LabQuest gas pressure probe and a temperature probe. The concepts of gas & liquid behavior, Dalton’s Law of partial pressures, intermolecular forces and colligative properties are used in this experiment. Calculations are based on density, moles, mole fraction, and Raoult’s Law.
Background Information
Consider a closed container at a given temperature that contains a liquid solvent. The molecules of the liquid are experiencing intermolecular forces that connect the molecules to each other in a cohesive force. The molecules are moving about throughout the liquid. However, some of the molecules will have enough kinetic energy to break the intermolecular forces holding it together as a liquid and “escape” to the gas phase. This process of molecules leaving the liquid phase and going to the gas phase is called evaporation. Generally, we refer to molecules in the gas phase as a vapor. As a vapor, these molecules generate a partial pressure. Some of the vapor molecules will condense back into the liquid phase. This process of molecules leaving the gas phase and going to the liquid phase is called condensation. At some time, the system will reach an equilibrium. At equilibrium, the rate of molecules undergoing evaporation is equal to the rate of molecules undergoing condensation. Both processes are still occurring, but the amount of molecules present as a vapor is constant. The partial pressure of the solvent molecules in the gas phase at equilibrium is called the vapor pressure.
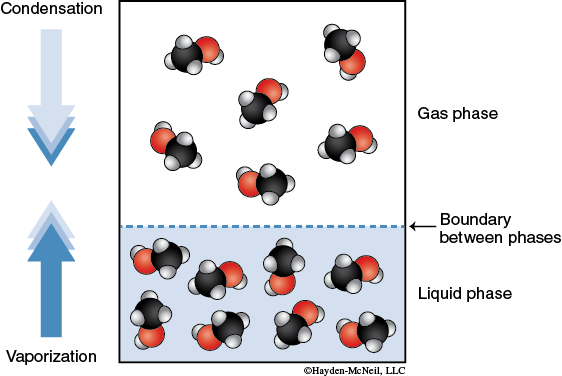
Compounds that easily convert from liquid to gas phase are said to be volatile. Volatility of a liquid depends on its molar mass (since it affects its kinetic energy) and intermolecular forces.
A solute (substance being added) is added to the volatile solvent (substance doing the dissolving) to form a solution (mixture). Some properties of the solution differ from the property of the pure solvent. Those properties of the solution that depend on the number of solute molecules in the solution and not on the identity of the solute, are called colligative properties. The vapor pressure, freezing point and boiling point are all colligative properties.
In looking specifically at vapor pressure, it has been observed that adding some solute to a solvent lowers the vapor pressure as compared to the vapor pressure of the pure solvent. This can be expressed mathematically in the equation below, which is called Raoult’s Law. The vapor pressure of the solvent over the solution (P) is equal to the mole fraction of solvent (Χsolvent ) multiplied by the vapor pressure of the pure solvent (P°).
Psolvent = Χsolvent P°pure solvent (Eq.1)
Pressures can be measured in several different units. Previously you have used units of torr, mmHg, and atm. However, the official SI unit of pressure is Pascal, abbreviated as Pa. There are 101,325 Pa in 1 atm. In this experiment, you will be measuring the pressures in kilopascals (kPa).
Example
Problem
What will be the vapor pressure of ethanol over a solution that contains 3.0 mL of ethylene glycol, C2H4(OH)2, and 7.0 mL of ethanol at 20°C?
The vapor pressure of pure ethanol (C2H5OH) at 20°C is 5.95 kPa Ethanol: density at 20°C = 0.789 g/mL; molar mass of ethanol = 46.07 g/mol Ethylene glycol: density at 20°C = 1.113 g/mL; molar mass = 62.07 g/mol
Psolvent = Χsolvent P°pure solvent
Solution:
(1) You will need to calculate the moles of both the ethanol and the ethylene glycol so that you determine the mole fraction of the ethanol. To find moles of a liquid one either needs its concentration or in the case of a pure solvent, its density.
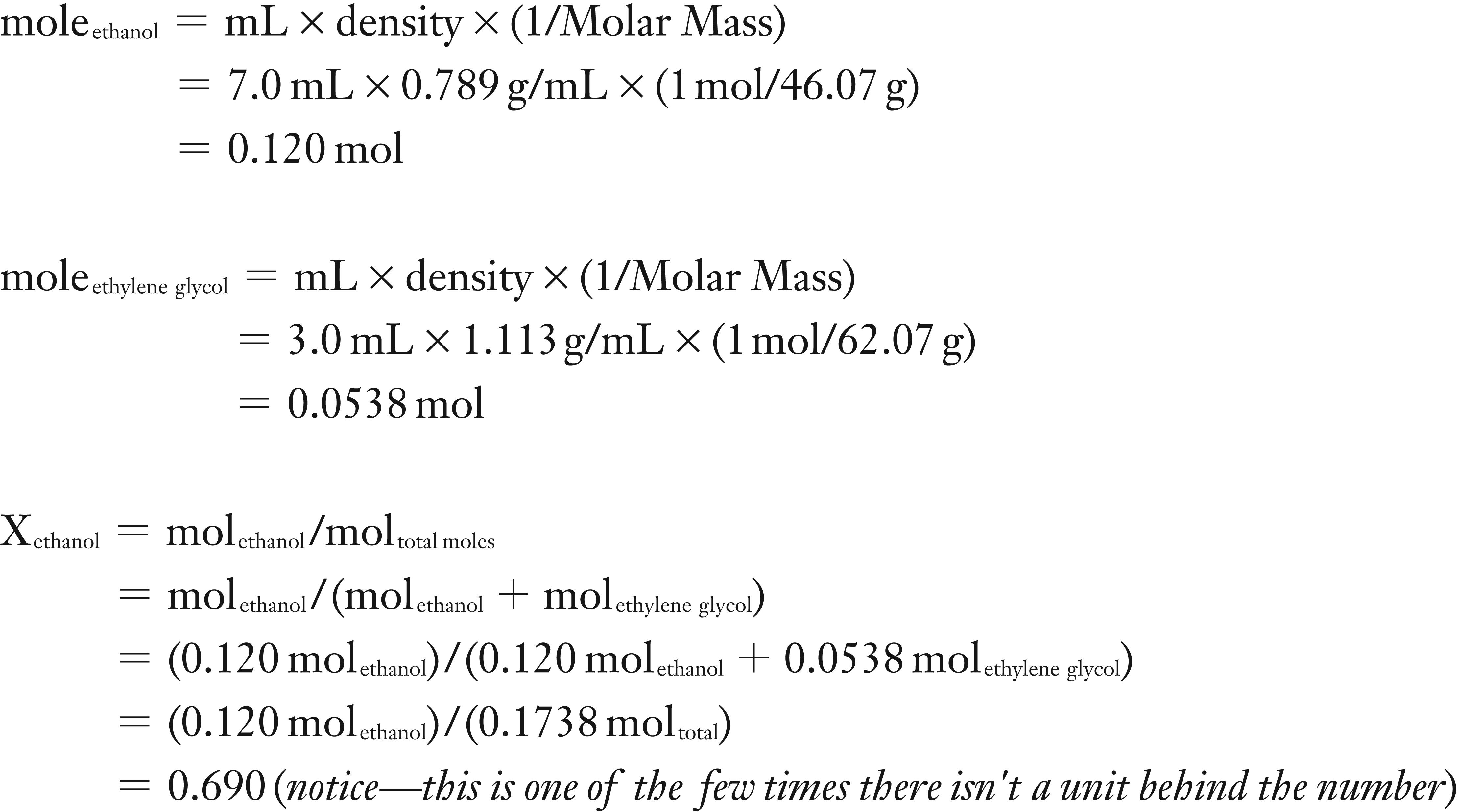
(2) Now you can use Raoult’s Law equation to solve for Pethanol.
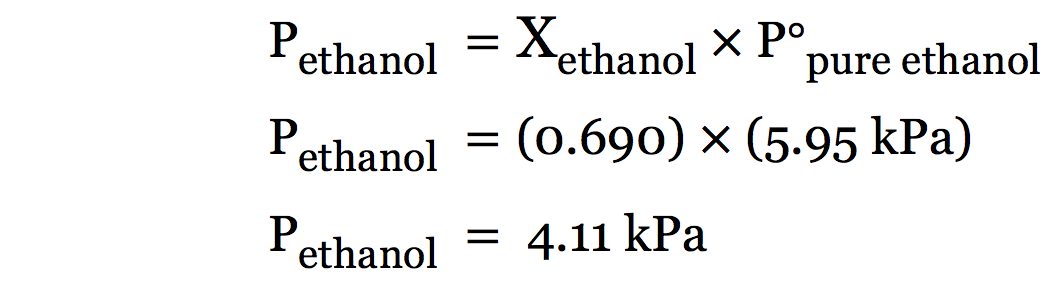
In This Experiment
In this experiment, you will measure the vapor pressure of a volatile, pure solvent (methanol) using a gas pressure sensor and a LabQuest. First you will measure the air pressure in the flask with the stopcock open so this is the atmospheric pressure. Second, you will add a sample of methanol to the flask and measure the pressure after the system has reached equilibrium. The total pressure inside the flask will increase due to the addition of the vapor pressure of methanol. Due the Dalton’s law of partial pressures, the total pressure in the flask is equal to the original air pressure plus the vapor pressure of pure methanol.
Ptotal = Pair + P°methanol (Eq. 2)
By rearranging the equation, you can find the vapor pressure of the pure methanol in Equation 3.
P°methanol = Ptotal – Pair (Eq. 3)
You will repeat the procedure to find the vapor pressures of two solutions of methanol. One solution will be a mixture of benzoic acid dissolved in methanol and the other solution will be a mixture of ethylene glycol in methanol. When determining the vapor pressure of methanol over each solution, you will determine Pmethanol (not P°).
Pmethanol = Ptotal – Pair (Eq. 4)
Last, you will compare your observed vapor pressure of methanol over a solution to the vapor pressures of methanol predicted by Raoult’s Law (Eq. 1). The colligative properties predict that the chemical nature of the solute doesn’t matter, just the amount of the solute.
Procedure
Always Wear Safety Goggles and Use Good Lab Practices
Chemical Alert:
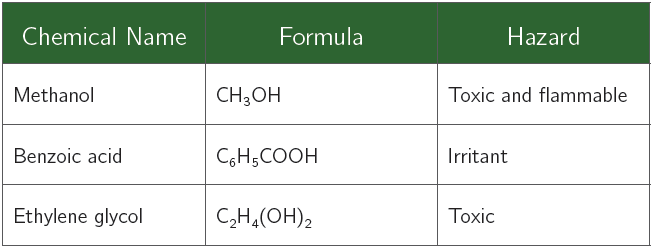
Part I
Set Up Experiment
1. Prepare a water bath by filling a 400 mL beaker with about 200 mL of water.
2. Connect a Temperature Probe to Channel 1 of the LabQuest.
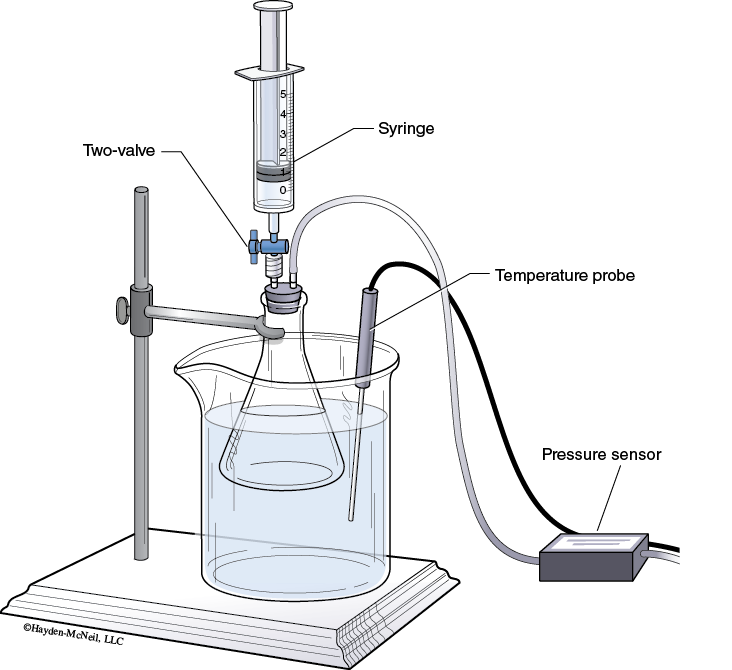
Connect a Gas Pressure Sensor to Channel 2 of the LabQuest.
The rubber-stopper assembly should have one piece of clear plastic tubing connecting back to the gas pressure sensor and a stop-cock valve in the other hole of the rubber stopper.
You will have two half-screens on the LabQuest. One for the temperature and one for the pressure.
3. Insert the white stopper snugly into the neck of a clean, dry 125 mL Erlenmeyer flask.
Place the Erlenmeyer flask in the water bath as shown in Figure 10-1.
Clamp the Erlenmeyer flask to a ring stand.
You may need to add or remove water from the beaker to get as much of the flask surrounded by the water.
4. Place the Temperature Probe in the water bath.
The temperature of the water bath should be close to room temperature.
5. Turn the two-way valve (above the rubber stopper) to the open position.
6. Obtain ~30 mL of methanol in a 50 mL beaker.
Part II
Determining P°methanol
7. Begin data collection by tapping PLAY (green triangle).
Collect data for about 30 seconds to obtain the initial temperature and pressure readings.
The atmospheric pressure should be in the 101 kPa region.
Record the pressure (Ptotal) and temperature.
8. Close the two-way valve.
Draw 3.0 mL of methanol into a 5 mL syringe.
With the two-way valve still closed, thread the syringe onto it (see Figure 10-1).
9. Open the valve below the syringe.
Push down on the plunger of the syringe to inject the methanol.
Quickly pull the plunger back to the 3 mL mark and close the two-way valve.
You will see a blip or a spike on the pressure graph corresponding to the injection.
10. Monitor the pressure and temperature readings.
End the data collection by tapping the red square button at 360 seconds.
11. Gently loosen and remove the stopper assembly from the flask. Unclamp the flask and pour the methanol into a waste beaker.
Turn the flask upside down on a towel to drain.
12. Drag the stylus over the highest 10 seconds of the pressure graph (highlights both graphs). Tap Analyze and then select Statistics and tap to select both temperature and pressure. (The statistics will show on the right side of the graph.)
Record the highest Pressure and average Temperature.
13. Reassemble the setup for a second trial and repeat steps 7–12, again injecting 3.0 mL of methanol.
The flask should be dry. If necessary blow air into the flask to finish evaporating the previous methanol.
Part III
Determination of Pmethanol from a Mixture
14. Tare the weight of a clean, dry 100 mL beaker. Add enough benzoic acid until you have approximately 3 grams. Record the exact weight of the benzoic acid.
15. Using the 10 mL syringe, transfer 10.0 mL of methanol to the beaker. Stir until the solid completely dissolves.
16. Reassemble the setup and repeat steps 7–12, using the 10 mL syringe to inject 3.0 mL of the mixture of methanol and benzoic acid (instead of the pure methanol).
17. Pour the mixture in the flask into your waster beaker.
Add a little bit of methanol to rinse the Erlenmeyer flask.
18. Reassemble the setup and repeat steps 7–12 again, injecting 3.0 mL of the methanol and benzoic acid mixture you made in step 16.
19. Pour all liquid waste into the waste container in the hood.
When methanol evaporates from the methanol and benzoic acid mixture, it leaves behind a white residue of the benzoic acid.
Wash all glassware with hot soapy water to dissolve any benzoic acid residue.
Rinse the syringes and return them to the back counter.
Data Analysis & Discussion
Calculations & Determination
Use Equation 3 and the data from Part II to calculate P°methanol for each trial. Average the two values of P°methanol.
Use Equation 4 and the data from Part III to calculate Pmethanol for each trial. (Remember that this time is for the mixture.)
Calculate the moles of methanol in Part III trials and the moles of benzoic acid in Part III trials. Calculate the Xmethanol.
The density of methanol is 0.792 g/mL.
Using Raoult’s Law (Equation 1), calculate Pmethanol using the average value of P°methanoland Xmethanol. Compare this value of Pmethanol to the average value of Pmethanol that you obtained experimentally.
Note any variance in the temperature during the experiments as this may be a source of error.
Study Questions
1. Know the definition of colligative properties, volatility, evaporation, condensation, mole fraction, and Raoult’s Law, solute and solvent.
2. Understand the different units of pressure: torr, atm, and Pascal & kilopascal.
3. Understand the difference between vapor pressure of a solvent over a solution (P or vp) and the vapor pressure of a solvent over pure solvent (P° or vpxolvent)
4. Calculate the mole fraction of methanol (CH3OH) in a mixture that is 8.10 mL methanol and 8.13 g benzoic acid (C6H5COOH). The density of methanol is 0.792 g/mL and its molar mass is 32.04 g/mol. The molar mass of benzoic acid is 122.12 g/mol and is a nonvolatile compound.
Using Raoult’s Law calculate the vapor pressure of methanol over the mixture above at 25°C. The P°methanol at 25°C is 16.9151 kPa.
5. Calculate the mole fraction of methanol (CH3OH) in a mixture that is 8.10 mL methanol and 3.72 mL ethylene glycol, C2H4(OH)2 The density of methanol is 0.792 g/mL and its molar mass is 32.04 g/mol. The density of ethylene glycol is 1.113 g/mL and its molar mass is 62.07 g/mol and is a nonvolatile compound.
Using Raoult’s Law calculate the vapor pressure of methanol over the mixture above at 25°C. The P°methanol at 25°C is 16.9151 kPa.
6. Using Raoult’s Law, predict the vapor pressure of ethanol (CH3CH2OH) over a solution that is a mixture of 11.00 mL of ethanol and 4.00 mL of ethylene glycol (C2H4(OH)2) at 20°C . The density of ethanol at 20°C is 0.789 g/mL and P°ethanol at 20°C is 5.95 kPa. The density of ethylene glycol 20°C is 1.113 g/mL and it is a nonvolatile compound.
7. Using Raoult’s Law, predict the vapor pressure of methanol (CH3OH) over a solution that is a mixture of 11.00 mL of ethanol and 2.00 g of benzoic acid (C6H5COOH) at 20°C . The density of methanol at 20°C is 0.792 g/mL and P°methanol at 20°C is 12.98 kPa. The benzoic acid is a white solid (molar mass = 122.12g/mol) and is a nonvolatile compound.
8. Raoult’s Law can be calculated in any units of pressure, such as kPa, torr, and atm. Using Raoult’s Law, predict the vapor pressure of water (H2O) in torr over a solution that is a mixture of 100.0 g of water and 15.0 g of sucrose (C12H22O11) at 65°C . The density of water at 65°C is 0.9806 g/mL and P°water at 65°C is 185.9 torr. The sucrose is a white solid and is a nonvolatile compound.
9. Callie & Gay & Steve discussed that if the mole fractions of the solvent are the same, it doesn’t matter that one solute is a solid and the other solute was a liquid. Is this true or false? Why or why not?
Activity Completed!