Chapter 1. Experiment 19
Oxidation-Reduction Titrations
Purpose of the Experiment
To determine the concentration of unknown solutions by titrating the unknown using an oxidation-reduction probe (ORP) in an oxidation-reduction reaction.
Background Required
This experiment will use basic laboratory titration techniques in a using a buret and LabQuest oxidation-reduction probe. The concepts of stoichiometry, titration, and oxidation-reduction reactions are used in this experiment. Calculations are based on stoichiometry.
Background Information
A titration is a process used to determine the volume of a solution needed to react with a given amount of another substance. The titrations in this experiment are based on oxidation-reduction reactions, which involves the transfer of electrons (e–). An oxidizing agent is the chemical which takes away electrons from the other reactant. For the two reactions to be analyzed in this experiment, you will use KMnO4, which is a common oxidizing agent. The KMnO4 will be the titrant (solution in the buret) in both reactions.
Since these are oxidation reduction reactions, the reaction equations must balance by number of atoms AND the number of e– transferred. One method of balancing the electrons, is the half-reaction method. The reaction is broken into two parts, the oxidation and reduction half reactions to see the gain and loss of electrons. In each half reaction, the number of electrons lost or gained, is determined by the change of oxidation number of one of the chemicals. Then the reduction and oxidation half reactions are added together after each has been multiplied (if needed) by the appropriate coefficient so that the electrons completely cancel each other.
For the first reaction, MnO4–(aq) reacts with Fe+2(aq) to form Mn+2(aq) and Fe+3(aq) in an acidic solution. The two half reactions are shown below.
MnO4–(aq) + 8 H+(aq) + 5 e– → Mn+2(aq) + 4 H2O(ℓ)
The Mn in MnO4– has an oxidation number of +7 and the Mn in Mn+2 is a +2. This is a 5 e– change, so note the 5 e– in the half reaction on the left side of the arrow. The oxidation number is decreasing, so it is a reduction half reaction.
Fe+2(aq) → Fe+3(aq) + e–
In this half reaction, it is easy to see that the Fe is going from a +2 to +3 oxidation number. This is an oxidation half reaction since the 1 electron is on the product side of the arrow. For the number of electrons to cancel each other out, this half reaction will need to be multiplied by 5 as shown below when it is added to the first half reaction.
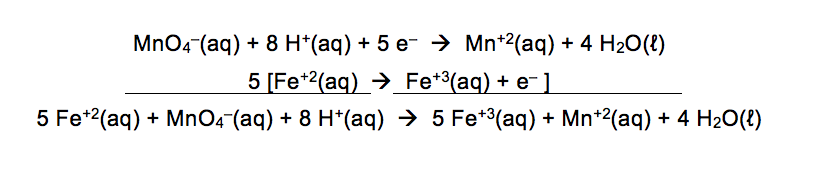
For the second reaction, MnO4–(aq) reacts with H2O2 (aq) to form Mn+2(aq) and O2(g) in an acidic solution.
MnO4–(aq) + 8 H+(aq) + 5 e– → Mn+2(aq) + 4 H2O(ℓ)
H2O2(aq) → O2(g) + 2 H+(aq) + 2 e–
In order for the electrons to cancel, the reduction half reaction will have to be multiplied by 2 and the oxidation half reaction will be have to multiplied by 5 to reach the least common denominator of 10. When the half reactions are added, the electrons will cancel and the number of H+ is simplified to obtain the reaction below.
5 H2O2(aq) + 2 MnO4–(aq) + 6 H+(aq) → 5 O2(g) + 2 Mn+2(aq) + 8 H2O(ℓ)
In This Experiment
In this experiment, an ORP (Oxidation-Reduction Potential) sensor will be used (instead of the conductivity sensor) to measure the electrical potential (millivolts, mV) of the reaction. The resulting electrical potential titration curve is similar in appearance to a pH titration curve of a strong acid solution titrated with a strong base (from lecture class). The change in Potential of the solution as the MnO4–(aq) is added is quite gradual until close to the equivalence point (when the reductant has completely reacted with the oxidizer). Near the equivalence point, the Potential changes very rapidly to produce an almost vertical line. The change in Potential then becomes more gradual again, before leveling off with the addition of excess MnO4–(aq). The center of the steep region is used as the equivalence point. The volume at this equivalence point is the equivalence point volume and it is this volume that is used in the titration calculations.
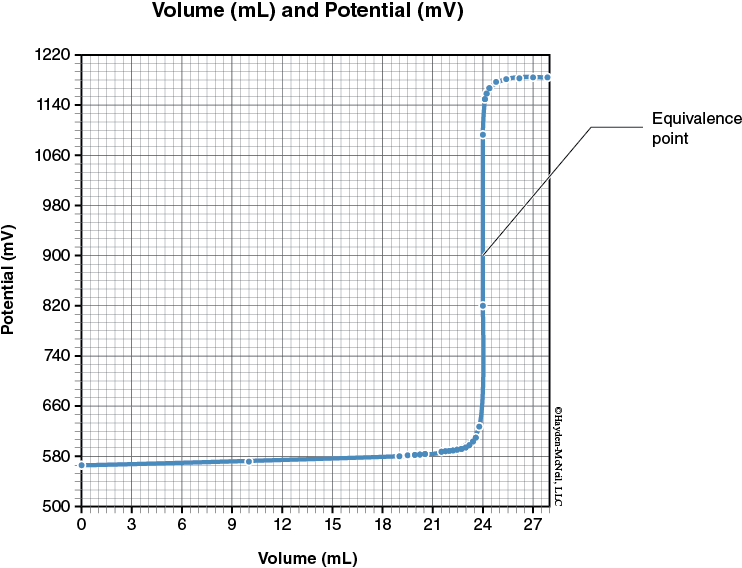
In the first reaction, you also monitor the reaction by the change in color of the solution. The ferrous ammonium sulfate solution (source of Fe+2 ions) is pale green, the Fe+3 solution is orange, and the MnO4– solution is dark purple. Initially the solution is green, then with the addition of the purple MnO4– forms the orange Fe+3 solution. After the equivalence point, the addition of the excess MnO4– will turn the solution a muddy brown. Since the color change is gradual, we need to plot the potential vs volume of MnO4– to determine the equivalence point instead of relying only on the color change.
In the second reaction, O2 bubbles form as one of the products. To minimize the accumulation of bubbles on the tip of the probe, the solution is stirred gently using the magnetic stirrer. Again, you can monitor the solution by color as well. The solution is initially colorless and after the endpoint, the addition of excess purple MnO4– will make the solution a light pink. Note the endpoint point by color (which is the first pink that stays) and compare it to the equivalence point from the graph.
Example:
Problem
What is the molarity of a Fe+2 solution that took 8.20 mL of 0.0400 M KMnO4 solution to reach the equivalence point when titrating 15.0 mL of the Fe+2 solution. (See balanced reaction on previous page.)
Solution
(1) Use the M & equivalence point volume of KMnO4 and stoichiometry to find moles of Fe+2.
(2) Then divide the moles of Fe+2 by the L of initial Fe+2 to find M of Fe+2.

.
Example:
Problem
What is the molarity of a H2O2 solution that took 15.7 mL of 0.0400 M KMnO4 solution to reach the equivalence point when titrating 2.00 mL of the H2O2 solution. (See balanced reaction on previous page.)
Solution
(1) Use the M & equivalence point volume of KMnO4 and stoichiometry to find moles of H2O2.
(2) Then divide the moles of H2O2 by the L of initial H2O2 to find M of H2O2.

Procedure
Always Wear Safety Goggles and Use Good Lab Practices
Chemical Alert:
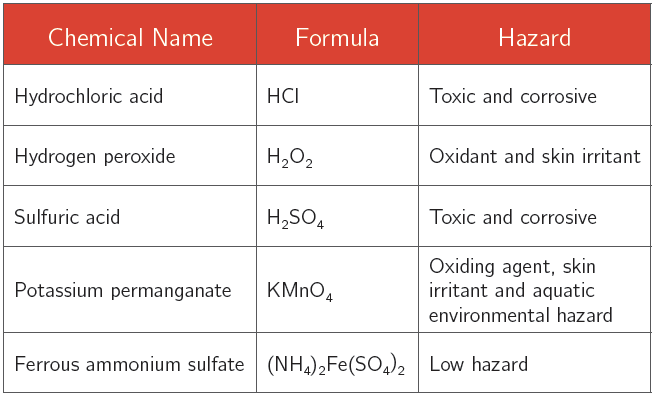
Part I
Titration of (NH4)2Fe(SO4)2 with MnO4–
1. Obtain ~15 mL of the ferrous ammonium sulfate unknown solution.
Use a syringe to transfer 10 mL of this solution into a 250 mL beaker.
Add 3 mL of 1.0 M HCl and 50 mL of deionized water to the beaker.
Place the beaker on a magnetic stirrer and add a stirring bar.
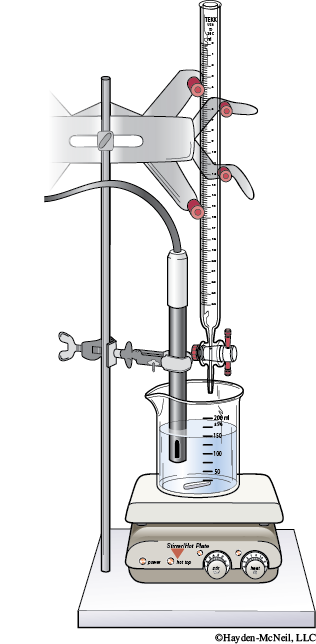
2. Obtain ~50 mL of 0.020 M KMnO4 solution.
Rinse a 25 mL buret with about 5 mL of the KMnO4 solution.
Attach the buret to the ring stand and then fill the buret.
3. Use the support arm or clamp to position the ORP Sensor so its tip is immersed in the solution but will not be struck by the stirring bar.
Adjust the speed of the stirrer so that it gently stirs the solution—no hurricane vortexes. The slight stirring mixes the solution.
4. Connect the ORP Sensor to the LabQuest.
Tap the MODE box on the LabQuest and then select Events with Entry from the pull-down menu.
Type in Volume of MnO4– in the NAME box and mL for UNITS.
Scroll down and tap the check box for Average over 10 seconds.
Tap OK.
5. Determine an initial potential reading before adding any MnO4– solution.
Tap PLAY (green triangle) to start collecting data.
Tap the KEEP button (will start 10-second countdown).
Then a prompt screen will appear to enter the volume of MnO4– added.
For this reading, enter “zero” and OK.
Record your initial buret reading.
6. Add ~0.5 mL of MnO4– to the solution and read the buret.
Tap KEEP (blue square) to start collecting data.
Enter the volume dispensed (current buret reading – initial buret reading).
Tap OK.
7. Repeat step 6, adding the MnO4– in ~0.5 mL increments.
(Each time, the volume of MnO4– is current buret reading – initial buret reading).
Note when different colors appear in the solution.
Stop when the potential value remains constant (about 15 mL) and tap STOP (red square).
At this point, the solution should have changed from green to orange to dark brown.
8. Tap a point in the center of the steep to determine the approximate volume needed to reach the equivalence point region.
Record the volume that corresponds to the equivalence point.
Record your data in your lab notebook.
Sometimes a contaminant is present which may give your graph two “humps.” If this happens, you want to focus on the steep area when the solution was orange.
9. Retrieve the magnet.
Pour the reaction mixture into the waste container in the hood.
Keep the MnO4– solution in the buret.
Part II
TItration of H2O2 with MnO4–
10. Obtain a small amount of 3% H2O2 in a beaker.
Transfer 0.70 mL of the H2O2 in solution to a clean 250 mL beaker.
Add 5 mL of H2SO4 and 90 mL of deionized water to the beaker.
Refill the buret with the 0.020 M MnO4–.
Set up the titration as in Part I, using a small magnet to gently stir the solution.
11. Start a new data set on the LabQuest. Repeat step 5 as before.
12. Add ~1.0 mL of MnO4– to the solution and read the buret.
Tap KEEP (blue square) to start collecting data.
Enter the volume dispensed (current buret reading – initial buret reading).
Tap OK.
13. Repeat step 6, adding the MnO4– in ~1.0mL increments until 9.0 mL have been added. Then add in 0.5 mL increments until the potential value remains constant. Then add two 1 mL additions.
(Each time, the volume of MnO4– is current buret reading – initial buret reading).
Note when different colors appear in the solution.
Stop when the potential value remains constant (about 15 mL) and tap STOP (red square).
At this point, the solution should be a pink-fuchsia color.
14. Tap a point in the center of the steep to determine the approximate volume needed to reach the equivalence point region.
Record the volume that corresponds to the equivalence point.
Record your data in your lab notebook.
15. Retrieve the magnet.
Pour the reaction mixture and any leftover MnO4– into the waste container in the hood.
Any acid or hydrogen peroxide solutions can be poured down the drain with running water.
Data Analysis & Discussion
Calculations and Determination
Part I: Titration of Fe2+
Use the volume at the equivalence point from the first titration to determine the Molarity of the unknown (NH4)2Fe(SO4)2 solution. Remember to look at the balanced redox reaction to find the mole:mole stoichiometric ratio.
What was the color of the solution at the equivalence point?
Part II: Titration of H2O2
Use the volume at the equivalence point from the second titration to determine the molarity of the H2O2 solution. Remember to look at the balanced redox reaction to find the mole:mole stoichiometric ratio.
What was the color of the solution at the equivalence point?
The concentration of commercial 3% H2O2 is 0.88 M.
Compare your M of H2O2 to this value.
Study Questions
Study Questions:
1. Write the balanced equation for the reaction of OCl– (in bleach) with H2O2. Determine how many e– were transferred in the overall reaction.
Hint: ClO– + H+ forms Cl– + H2O for one half reaction and the other half reaction is for the H2O2shown earlier. You will need to balance the first half reaction.
2. In a similar experiment to Part I, Ferris, Mona, Sully, & Fay determined the equivalence point volume was 12.5 mL of 0.025 M KMnO4 when titrating a 15.0 mL sample of (NH4)2FeSO4. What is the Molarity of the (NH4)2FeSO4 solution?
3. Ferris thought the calculations should have 1:1 mole ratio, since there was only 1 electron change in the Fe+2 to Fe+3. Is he correct? If not, explain what the ratio should be?
4. Mona thought they could do the titration based on color of the solution and not need the ORP probe. Based on your work, is she correct?
5. Perry, Ox and Ida did the same titration as in Part II with the H2O2. They determined the Molarity of the hydrogen peroxide as 0.99 M. What is the % error for their value as compared to 0.88 M H2O2 (of 3% solution)?
6. In Part I, which chemical was the oxidizing agent and what chemical was oxidized?
7. In Part II, which chemical was the oxidizing agent and what chemical was oxidized?
Activity Completed!