Chapter 7. Determining Planetary Interiors

7.1 Introduction

The goal of this module: Be able to determine the interior structure of a planet from its density and mass.

Why you are doing it: Knowing the interior structure answers other questions about the planet, for example, why Mars has a weak magnetic field and why Jupiter has such a strong magnetic field.

Background: Like detectives sifting through limited clues in order to solve subtle cases they did not witness firsthand, astronomers must use the limited data they have to draw conclusions about properties of astronomical bodies that cannot be directly observed. The interiors of planets is a good case in point. We cannot see into any planet, but from the observations we can make, it is possible to infer their internal compositions. One powerful technique astronomers have for doing this is to determine the average density of each planet and use that data to deduce its interior chemistry.

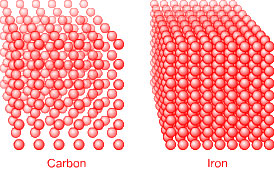
Density is the mass of an object divided by its volume. This is a useful parameter because every element and every chemical compound has a different density. For example, a cube of iron one meter on each side has more mass, i.e., particles (protons, neutrons, and electrons) packed into it than does a cube of carbon with the same volume. Therefore, iron is denser than carbon.

Every planet in our solar system is composed of varieties of elements, with different ones concentrated at different depths. The separation between rock and metal or any other pair of substances in a planet occurs because higher density objects sink below lower density ones. This is also why a rock sinks to the bottom of a pond. All the planets have their densest elements at their centers or cores, with shells of consecutively lighter elements layered above. We describe this by saying that all the planets of our solar system are differentiated - different substances are in different layers.

Since every planet contains a variety of substances, we can only directly calculate the average density of a world; Adding up all its mass and dividing by its total volume yields each world's average density. When this is known, we can work backwards to infer what substances that world contains.

7.2 Average Density

The average density of any object is simply the total amount of matter it contains (its mass) divided by its volume. Mathematically this reads:

For this tutorial, we divide the masses into 4 categories: very low mass, low mass, moderate mass, and high mass. Of the eight planets in the Solar System, two planets can be placed into each of these four categories.

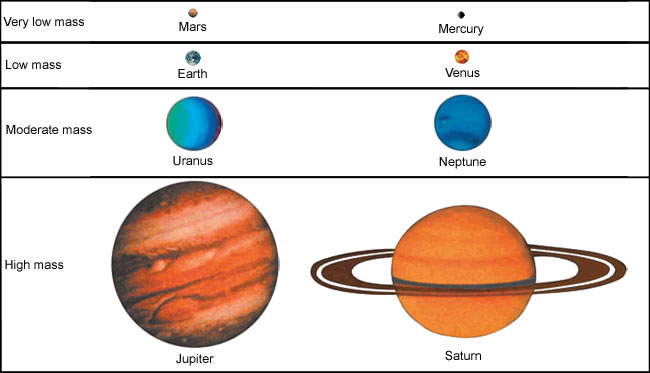
As a practical example, we will determine the density of the Earth and interpret this number in terms of possible planetary interiors, after which you will do the same for other planets on your own.

7.3 Determining a Planet's Volume

Since the planets are nearly spherical, the volume of a sphere, V, is described well by the equation \(V= \frac{4}{3} \pi r^{3} \) , where r is the planet's radius. In our example, r is Earth's radius, \( R_{ \bigoplus } \). Rather than looking this up in a book, you will make observations with this tutorial to determine the radius of Earth and the other worlds. These are analogous to actual observations that first determined the volumes of planets.

Here is how you find the radius: imagine that you are in a spaceship far enough from each planet to see it as a disk on the sky. This distance from your spacecraft to the planet, l, will be provided for each planet.

Use the Angle Measurer: grab and drag the left-side vertex (at the +) until it is on the edge of the planet. This observation will provide you with the angle, θ, between the center and edge of the planet, Earth in this example, as seen from your spaceship.

Because your observation creates a right triangle, we can use the equation for the tangent to find the radius of the planet, r. To do this, recall that we know your distance to the planet, l and the angle θfrom the center of the planet to its edge, so \( tan\hspace{1 mm} \theta = \frac{r}{l} \) or \( r = l\hspace{1 mm} tan\hspace{1 mm} θ \). The units for the angle(θ) are degrees(°), for distance(l) meters(m), and the radius calculated will also be in meters. You will not have to do this calculation, just plug in the values you were given for l and measured for θ into the Radius Calculator below to get r.

Radius Calculator

Radius Calculator

Radius (r) = l tan θ = tan
Radius = ? meters

Type the result you get for r into the radius slot of the Volume Calculator.

Volume Calculator

Volume = \(\frac{4}{3} \pi r^{3} \), r = (m)
Volume = ? m³

Density Calculator

=

kg m3

average density = ? kg/m³

Be sure to make a note of your results!

7.4 Determining a Planet's Density

Now plug the mass and volume into the Density Calculator to get the Earth's average density (in kg/m³, 3 significant figures).

Be sure to make a note of your results!

Before trying to identify the Earth's interior, please read and consider the following fine print and guidelines concerning planetary interiors:

The following two points will help you select planetary interiors.

1. Terrestrial Cores Astronomers believe that each planet, whether mostly hydrogen and helium, mostly water, mostly rock, or mostly metal, was initially a rock and metal body whose gravitational attraction pulled onto itself other substances in its environment. Therefore, all planets have terrestrial (rock and metallic) cores.
2. Gravitational Compression As mass piles up to create a planet, the inward gravitational force of all this material compresses the matter in the interior. Therefore, the densities of elements and compounds deep inside every world are greater than are the densities of the same materials on the planet's surface. Indeed, the pressures inside Jupiter and Saturn are so great that much of their interior hydrogen is converted into an excellent conductor of electricity called liquid, metallic hydrogen. This version of hydrogen has a much higher density than liquid hydrogen in the outer layers of any world. (It is a million times denser than the air you breathe). The greater the planet's mass, the more its interior is compressed to higher densities.

Important clue: When you look at the possible interiors coming up, check the mass of the planet you are considering to see how much its interior substances are being compressed. For example: Jupiter, with 318 Earth masses, can compress its interior hydrogen to more than 1000 kg/m³ (the density of water on the Earth's surface) whereas Uranus, with only 19 Earth masses cannot compress hydrogen to nearly this density. Likewise, water inside Jupiter is compressed to well over 2000 kg/m³. If most of that planet's interior is water, then its density would be over 2000 kg/m³.

7.5 Inferring a Planet's Interior Chemistry from its Density

In order to use the average density to propose a model of a planet's interior, here are the general rules for 'building' planetary interiors based on the fine print you have just read.

• If its average density is less than about 2000 kg/m³ (twice the density of water on the surface of the Earth), then a very low-mass, low-mass, or moderate-mass planet is likely to contain a lot of water, along with much hydrogen and helium. A high-mass planet is likely to contain mostly hydrogen and helium, with a relatively small amount of water.
• If its average density is between about 2000 kg/m³ and about 5000 kg/m³, then a very low mass world would be made mostly of moderate-density elements such as oxygen, silicon, magnesium, and carbon. A low-mass planet in this density range would contain large amounts of both these moderate-density elements and water. A moderate or high mass world in this density range would contain large amounts of hydrogen, helium, water, and moderate-density elements.
• If its average density is between about 5000 kg/m³ and about 8000 kg/m³, then a very low mass world would be made mostly of high-density elements like iron and nickel. A low-mass world would contain large amounts of both moderate-density elements and high-density elements. A moderate-mass world in this density range would have large amounts of water and moderate density elements. A high-mass world in this density range would have large amounts of hydrogen, helium, water, and moderate-density elements.
• If its average density is higher than about 8000 kg/m³, then very low and low-mass planets would be composed primarily of high density elements, while moderate and high-mass planets would have both moderate and high-density elements.

These four bulleted points are summarized in the table above.

7.6 Choosing an Interior

Question 7.1

From the density that you have calculated and the discussion above about planetary interiors, click on the cutaway interior from the choices below that you believe most accurately represents the Earth.

Refer to the Density/Mass Category Table.

nI+EIf4JBr2DpLGlxyqHP9qWbzncaZL2kBBpwdVCucjLCBlLgdITbW5Xu0KUA6mUAjxrhg==

3

Try again.

Correct. An Earth-sized world with such a mix of high and medium mass elements would have a density of around 5500 kg/m³.

Incorrect. An Earth-sized world with such a mix of high and medium mass elements would have a density of around 5500 kg/m³.

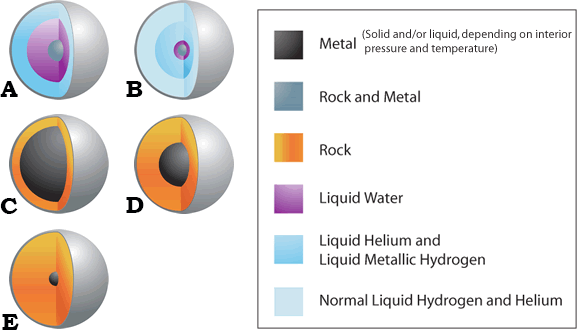
7.7 Choosing an Interior - Mars

Question 7.2

Repeat the process for Mars and choose the cutaway interior you believe most accurately represents Mars.

Use Measurements, Calculations, and the Density/Mass Category Table.

AHM1ElXYEtViDMIJ/S7nWaD19SbHLxXzU/1CEEzO1Aw+KIKkHJ9CwU+QP4no3hJR41WKdg==

3

Try again.

Correct. A Mars-sized world composed mostly of moderate density elements would have a much lower average density than that of the Earth.

Incorrect. A Mars-sized world composed mostly of moderate density elements would have a much lower average density than that of the Earth.

7.8 Choosing an Interior - Saturn

Question 7.3

Repeat the process for Saturn and choose the cutaway interior you believe most accurately represents Saturn.

Use Measurements, Calculations, and the Density/Mass Category Table.

PTi4yKYqSPn7Yh6NolTIzWJEi3wEeD1gbKryOSZlZpmTz/E5cxW1ZEP2L172t3JiHkEApw==

3

Try again.

Correct. A high mass planet like Saturn compresses much of its hydrogen into the liquid metallic state, with an average density roughly that of water.

Incorrect. A high mass planet like Saturn compresses much of its hydrogen into the liquid metallic state, with an average density roughly that of water.

7.9 Quick Check Quiz

Determine the inner structure of the remainder of the planets, using the densities listed in each question and the Density/Mass Category Table. Suggestion: compare the densities that you get for these worlds with the density of the Earth that you derived previously.

Question 7.9

Mercury (density: 5430 kg/m³):

OywPD2tftI8hhZ5IZ3D0vzkRitTfaXkC1xMENexxJKyvQenm+jdJcIadtNY=

Correct. A Mercury-sized world composed mostly of moderate density elements would have a much lower average density than that of the Earth.

Incorrect. A Mercury-sized world composed mostly of moderate density elements would have a much lower average density than that of the Earth.

Question 7.10

Venus (density: 5240 kg/m³):

0B+K4GeD7qNIt+0+Qj34NOzjx0ZSZEpCeDepCN24To0VslSFTQ5WVzjhTsU=

Correct. A Venus-sized world of water, hydrogen, and helium would have an average density of less than 2000 kg/m³. At Venus's distance from the Sun, its hydrogen and helium would quickly evaporate.

Incorrect. A Venus-sized world of water, hydrogen, and helium would have an average density of less than 2000 kg/m³. At Venus's distance from the Sun, its hydrogen and helium would quickly evaporate.

Question 7.11

Jupiter (density: 1330 kg/m³):

smNZLpEyUUDmM+9b/LqCxhC1P8Bg7wn8FpVt791lO34PoqHFzFtLcfwdN0Y=

Correct. A high mass planet like Jupiter compresses much of its hydrogen into the liquid metallic state, with an average density roughly that of water.

Incorrect. A high mass planet like Jupiter compresses much of its hydrogen into the liquid metallic state, with an average density roughly that of water.

Question 7.12

Uranus (density: 1320 kg/m³):

8Lx4k+SzPjyfvoXaLHgqQEkTkYeLqUWnz8bJUewg/tCrcFqgoUHyv4zJeqE=

Correct. A moderate-mass planet like Uranus composed of high and moderate mass elements would have an average density above 10,000 kg/m³.

Incorrect. A moderate-mass planet like Uranus composed of high and moderate mass elements would have an average density above 10,000 kg/m³.

Question 7.13

Neptune (density: 1640 kg/m³):

8Lx4k+SzPjyfvoXaLHgqQEkTkYeLqUWnz8bJUewg/tCrcFqgoUHyv4zJeqE=

Correct. A moderate-mass planet like Neptune composed mostly of high mass elements would have an average density above 10,000 kg/m³.

Incorrect. A moderate-mass planet like Neptune composed mostly of high mass elements would have an average density above 10,000 kg/m³.