Chapter 22. The Nature of Black Holes

22.1 Introduction

An artist's conception showing what happens when a star wanders too close to a black hole and becomes captured by its gravity. What exactly is a black hole and how do they form?

The goals of this module: After completing this exercise, you should be able to:

1. Explain what needs to occur in order for a star to end its life as a black hole.
2. Describe the physical nature of a black hole, as well as the region surrounding it.
3. Calculate the Schwarzschild radius for a black hole of a given mass.

In this module you will explore:

1. How massive objects curve space.
2. How the speed needed to escape the gravitational pull of an object depends on its mass, as well as your distance from it.
3. Which properties of a black hole can be determined.

Why you are doing it: Black holes are probably one of the most fascinating objects in the entire universe, and yet one of the least understood. Because of this, black holes have become the object of many science fiction stories. In this activity, you will explore how a black hole forms, and discover what science teaches us about them.

22.2 Background

Supernova SN 2006gy, the explosion of a supermassive star, possibly 150 times more massive than our Sun, will undoubtedly result in the formation of a black hole from the remains of its core.

As a star nears the end of its life, it runs out of fuel in its core, and nuclear reactions cease. When this happens, the gravity of the star causes the core to collapse inward while the star's outer layers are expelled (either in a planetary nebula or a supernova event). The remaining mass will then collapse to form one of three stellar remnants, depending on how much mass is present.

If the remaining mass is below 1.4 solar masses then, as the core collapses, the electrons will be compressed so tightly that they will start exerting an outward pressure which stabilizes the collapse of the star, forming a white dwarf. Above 1.4 solar masses (but somewhere below about 3 solar masses), gravity is strong enough to overcome this electron degeneracy pressure, and force the core to collapse even further. Eventually, the collapse is halted by a neutron degeneracy pressure (due to the neutrons being packed as tightly as possible), and a neutron star forms.

But what if the core that collapses is even more massive? Above 3 solar masses, the gravity of the star that causes the collapse is so strong that not even neutron degeneracy pressure is strong enough to halt it, and the star continues to collapse. At this point nothing stops the collapse of the star, and a black hole is formed.

22.3 Mass Curves Space

Before we explore exactly what a black hole is, we first need to investigate the concept of gravity a little further.

Summary

In the 1900's, though, our understanding of gravity changed when Albert Einstein introduced his theory of general relativity. Among his many ideas, Einstein theorized that gravity is really a manifestation of the curvature of space due to the presence of massive objects. Think of space as a two-dimensional rubber sheet. An object rolls across it in a straight line. Now, place an object with mass on the sheet. What happens? The massive object distorts the sheet as shown in the figure above. As you try to roll an object across the sheet, if it rolls too close to the massive object, its path is deflected around the massive object; the more massive the object, the greater the deflection. This is how Einstein explained gravity.

Gravitational Curvature

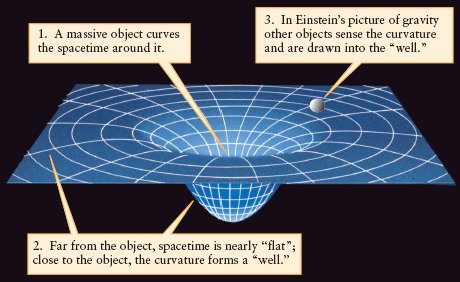
So what is the difference between Newton's law of gravity and Einstein's? According to Newton, gravity is a force between two objects of mass. According to Einstein, gravity is due to the presence of one massive object; regardless of the second object. Therefore, gravity can affect objects without mass, such as photons of light.

22.4 Observational Evidence of General Relativity

So how do we know that Einstein was right? We have observational evidence. Follow the animation below.

22.5 Black Holes: A Point Singularity

So let's go back to the black hole. As you may recall, in the case of a black hole, the core is massive enough such that nothing can halt the gravitational collapse of the stellar remains. Gravity keeps pulling everything inward until the entire mass has collapsed down to a point, known as a singularity. Let us emphasize this: The entire mass of the black hole is contained in a point of zero volume.

Question 22.5

lgrQFY8w/tk50mgZIFf8bZ6NS2CKg7MAvE9AJrmNqxkOB+OuLQ6/J4p1OQ5iDmkZTPylrEbxySw2YYPejmnSU9MN1CZ2gTGescZyqjl/trlm7Kz4zUV6imLx9alC/XVkFNvrXGsePfxQCUvG7Lu7XNlWu/0rW+XkGXJi/voLj7o8Qi1fWecUDc9bOXj3WSS8I6NeSkx/f1nNQdKlyTk+66LBmTyE3nac

3

Try again. Since the entire mass of the black hole is collapsed down into a point, it has zero volume. Any number divided by zero equals infinity. Therefore, black holes have an infinite density.

Formation of a black hole.

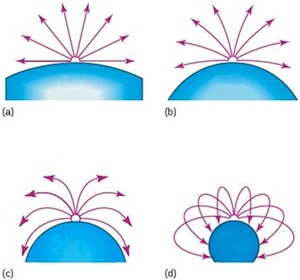
As the remains of a star collapses to form a black hole, the density of the remnant becomes higher and higher. According to Einstein's theory of relativity, this curves the space around it more and more. Look at the figure to the right. As the mass is compressed into smaller and smaller volumes, the path of light traveling from the surface becomes more and more curved. As the object collapses into a black hole, space becomes so highly curved that the beams of light curve back onto the black hole, such that not even light can escape its gravitational pull. If we use the same model of a rubber sheet to represent space as we did before, we can think of a black hole as being so massive that it creates a hole infinitely deep, such that if anything (including light) passes too close, it will fall into the black hole and never escape.

Correct. Since the black hole has zero volume, any number divided by zero equals infinity. Therefore, black holes have an infinite density.

Formation of a black hole.

As the remains of a star collapses to form a black hole, the density of the remnant becomes higher and higher. According to Einstein's theory of relativity, this curves the space around it more and more. Look at the figure to the right. As the mass is compressed into smaller and smaller volumes, the path of light traveling from the surface becomes more and more curved. As the object collapses into a black hole, space becomes so highly curved that the beams of light curve back onto the black hole, such that not even light can escape its gravitational pull. If we use the same model of a rubber sheet to represent space as we did before, we can think of a black hole as being so massive that it creates a hole infinitely deep, such that if anything (including light) passes too close, it will fall into the black hole and never escape.

Incorrect. Since the black hole has zero volume, any number divided by zero equals infinity. Therefore, black holes have an infinite density.

Formation of a black hole.

As the remains of a star collapses to form a black hole, the density of the remnant becomes higher and higher. According to Einstein's theory of relativity, this curves the space around it more and more. Look at the figure to the right. As the mass is compressed into smaller and smaller volumes, the path of light traveling from the surface becomes more and more curved. As the object collapses into a black hole, space becomes so highly curved that the beams of light curve back onto the black hole, such that not even light can escape its gravitational pull. If we use the same model of a rubber sheet to represent space as we did before, we can think of a black hole as being so massive that it creates a hole infinitely deep, such that if anything (including light) passes too close, it will fall into the black hole and never escape.

Explore what happens to objects near a black hole in the animation. To begin - set the initial position using the slider and press "Go."

22.6 The Extent of a Black Hole

Structure of a black hole

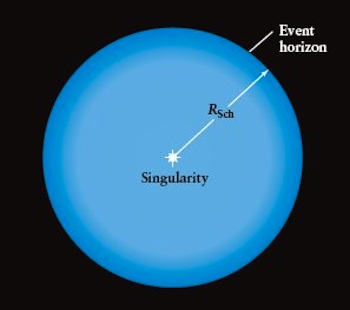
While in theory a black hole is simply contained in a point volume of infinite density, astronomers define a radius for the black hole called the Schwarzschild radius. To understand how the Schwarzschild radius is determined, we first need to consider the concept of escape speed.

Basically, escape speed is defined as the speed at which an object needs to travel in order to escape the gravitational pull of another object. According to Newton’s Law of Universal Gravitation, the gravitational force increases as the mass of an object increases, and decreases as your distance from it increases. Therefore, it makes sense that the speed at which you need to move in order to escape from the gravitational pull of an object also increases as the mass of the object increases, and decreases the farther you are from it. The exact formula for escape speed is

where G is the gravitational constant, M is the mass of the object from which you are trying to escape, and R is your distance from it. For example, in order for an object to free itself from the gravitational pull of Earth, it must have an escape velocity of 11.2 km/s. The space shuttle leaving Earth doesn’t move quite this fast because a shuttle is not trying to leave Earth’s gravitational pull, just orbit around it.

For a black hole, if you are right next to it, the escape speed is so high it is greater than the speed of light. Not even light can escape from a black hole. But as we pointed out in the formula above, the farther away you are from the black hole, the lower the escape speed. The Schwarzschild radius is defined as the distance from an object at which the escape speed equals the speed of light. Therefore, inside the Schwarzschild radius, nothing can escape a black hole. Outside of the Schwarzschild radius, if you are moving fast enough, it is possible to escape from the black hole's gravitational pull. Astronomers define the region surrounding a black hole with a radius equal to the Schwarzschild radius as the event horizon. Look at the figure above to locate the event horizon. Anything inside of the event horizon is trapped forever. Outside of the event horizon, if you are moving fast enough, you can escape from a black hole's pull. The Schwarzschild radius that defines the extent of the event horizon is given by:

where c is the speed of light. As you can see, the more massive the black hole is, the larger its event horizon. An easy rule of thumb is that a 1 solar mass object has a Schwarzschild radius equal to 3 km, and the Schwarzschild radius scales directly with the mass.

22.7 The Power of a Black Hole

What if the sun were replaced by a black hole?

It is a common misconception that black holes in space sit around "sucking up" any object that is around them. This is simply not so. Black holes, like any other object with mass, simply exert gravitational forces on other objects, distorting their paths, possibly to the point that they become gravitationally bound to the black hole and eventually fall into it. But this is true of any massive object. There is only one major difference between black holes and other massive objects.

22.8 Properties of a Black Hole

Structure of a rotating black hole

Since not even light can escape from within the event horizon of a black hole, we have no idea what space is like inside of one. The only way we know anything about space is from the light we receive from the objects in it; if we don't receive any light from a black hole itself, there is no way of knowing what a black hole (the point singularity) is like. Unfortunately, our knowledge of physics simply is inadequate in this situation.

Fortunately, though, there are a few properties of a black hole we can determine. The first, and most obvious, is its mass. How do we determine the mass of a black hole? We observe how it gravitationally influences nearby objects. If we can observe objects in orbit around a black hole and see how its motion is directed by the gravity of a black hole, we can calculate a black hole's mass.

Second, we can determine a black hole's electric charge. The mass that went into creating a black hole was composed of electrons and protons, both of which carry a charge. According to the laws of physics, electric charge can neither be created nor destroyed; therefore, whatever charge the mass had before collapsing, it has after collapsing. Like gravity, electric forces obey an inverse squared relation with distance (the strength of the force drops as the inverse square of the distance). Therefore, if a black hole has an electric charge, it can be measured.

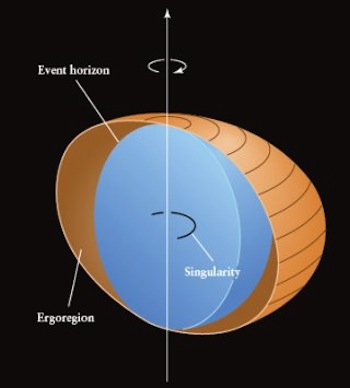
Third, we can determine a black hole's angular momentum. As a spinning object collapses, and its mass moves closer to its rotation axis, the object begins spinning faster and faster. This is due to the Law of Conservation of Angular Momentum. In other words, the angular momentum of the object stays the same, unless an external force acts on the object to change it. Ice skaters have a wonderful understanding of the conservation of angular momentum. When they go into a spin, they start with their arms spread out, distributing their mass far from their rotational axis, and spin slowly. As they pull their arms in, their mass moves closer to their rotational axis, and they spin faster. Since no external force acts on the collapsing star, its angular momentum remains constant and it spins faster as it gets smaller.

So how do we measure the angular momentum of a black hole? It turns out that, as a black hole rotates, it pulls the space nearby around with it (this effect has actually been detected due to the Earth's rotation). This region of space is known as the ergoregion, depicted in the illustration above. Since the ergoregion lies outside of the event horizon, if we could pass a space probe through this region, we could measure the effect the black hole's rotation has on the space probe, and from that, determine its angular momentum.

22.9 Quick Check

Indepth Activity: The Nature of Black Holes