Chapter 24. The Distance Ladder

24.1 Introduction

A Hubble Space Telescope image reveals galaxies in the constellation of Hercules (the ones shown in boxes are roughly 11 billions light years away from us).

The goals of this module: After completing this exercise, you should be able to:

1. Explain how various techniques are used to measure distances to galaxies.
2. Describe what makes an object a good standard candle.
3. Explain how the uncertainty of distance measurements increases with distance.

In this module you will explore:

1. How the luminosities of a variety of objects are determined.
2. How luminosity is used to calculate distance with the inverse square law of light.
3. How astronomers use the distances to nearby objects to determine distances to farther objects.

Why you are doing it: When we look out into the heavens, one of the questions that always fills us with awe is "Just how big is the universe?" To determine the answer to this question, a number of techniques are used to measure distances to farther and farther galaxies. Ultimately we would like to determine the size of the universe itself.

24.2 Background

Stellar parallax can be used to measure distances to the nearest stars.

When astronomers first observed other galaxies, there was a debate as to whether they were "spiral nebulae" located within the Milky Way or if they were "island universes" outside the bounds of our Galaxy. To help resolve this, astronomers developed a number of distance measurement techniques to objects farther and farther away.

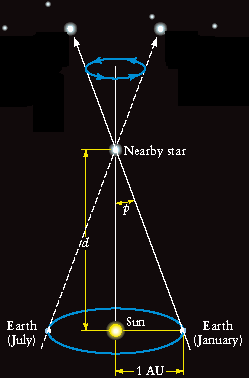
Within our local neighborhood of stars, we can use stellar parallax to measure distances to nearby objects. Stellar parallax, as you may recall, is an apparent shift in the position of a nearby objects relative to background objects due to a change in perspective of the observer. The farther away an object is, the smaller its parallax. As the Earth moves around the Sun, nearby objects appear to shift back and forth over the span of a year. By measuring this apparent shift, we can determine distances to nearby stars. With the Hipparcos satellite, we measured accurate distances using stellar parallax out to about 500 pc away.

Once astronomers displayed stellar properties on an H-R diagram, they found that it could be used as a distance indicator as well, through a process known as Spectroscopic Parallax. Given a well-defined H-R diagram, if you observe a star of known spectral type and luminosity class (like main sequence or red giant, which can be determined by examination of the width of the spectral lines), you can determine its position on the H-R diagram. Determining its luminosity is then as simple as reading it off of the axis. Once you know the star's luminosity, you can observe its apparent brightness, and then use the inverse square law of light to determine its distance. This method is useful out to a distance of about 10 kpc (10,000 parsecs).

24.3 Cepheid Variables

A Cepheid Variable detected in M100 allows astronomers to determine a distance of 17 Mpc (17 million parsecs) to this galaxy.

In 1908, while cataloguing the brightnesses of stars in the Small Magellanic Cloud, Henrietta Leavitt noted that a number of stars varied in brightness, and that their period of variation was directly related to their apparent brightness. Once the distance to the Small Magellanic Cloud was determined, the apparent brightnesses were converted into luminosities, and a Period-Luminosity relation was derived. For this particular type of star, known as Cepheid variables after the first of its type to be observed - δ Cephei, the Period-Luminosity relation states that the longer the period of variability, the more luminous the star on average. Cepheid Variables are useful distance indicators, since their periods of variability give us their luminosities.

24.4 Tully-Fisher Relation

In 1977, two astronomers, R. Brent Tully and J. Richard Fisher discovered a relationship for spiral galaxies, which also provides a useful distance indicator. They discovered a strong correlation between two galactic properties. It turns out that the rotation speed of a spiral galaxy is highly correlated with its total luminosity. Based on this relation, if you can measure the rotation speed of a spiral galaxy, then you can determine its luminosity. Then, you observe its apparent brightness and use the inverse square law of light to determine its distance.

How do you determine the rotation speed of a galaxy? As a galaxy rotates, one side of the galaxy is moving towards us, while the other side is moving away. Cool hydrogen gas in the galaxy emits 21-cm radiation, but as the gas moves either towards us or away from us, the light it emits is Doppler shifted to either longer or shorter wavelength, a redshift or a blueshift. As we observe the total light from a galaxy, we see all of the light emitted from the hydrogen gas in the galaxy at the same time.

The animation above depicts a rotating spiral galaxy giving off light at 21 cm. The side moving towards us is blueshifted while the side moving away from us is redshifted. At the top of the animation is a slide that will allow you to adjust the rotation speed of the galaxy. Use the slider to change the speed such that the galaxy spins faster. Observe the effects on the spectral line. Then change the speed such that the galaxy spins slower.

24.5 Faber-Jackson Relation

Elliptical galaxies don't spin, so astronomers found another method for measuring distances to these galaxies.

While the Tully-Fisher relation is useful in spiral galaxies, it cannot be used with elliptical galaxies, like M87 shown to the right, because ellipticals do not rotate in an orderly fashion. Stars orbit, but in a variety of directions and orientations. Fortunately, a similar method, known as the Faber-Jackson relation, can be used with them. Although elliptical galaxies do not rotate, the stars within them still have orbits through the galaxy. According to the Faber-Jackson relation, the total luminosity of an elliptical galaxy is correlated with the dispersion of velocities (deviations from the average velocity) of stars near the center of the galaxy; the greater the dispersion, the more luminous the galaxy. Therefore, by using the Doppler effect to measure the various speeds of the stars and determining how they deviate from the average motion, we can use the Faber-Jackson relation to determine the luminosity of the galaxy. Then, by measuring the galaxy's apparent brightness, we can use the inverse square law of light to determine its distance.

24.6 Type Ia Supernovae

In 2006, a Type Ia Supernova was detected in M100, shown here before and after the event. (The two images were taken with different filters, hence the color difference).

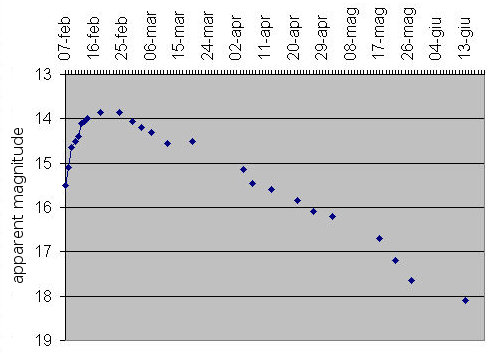
One of the most useful distance indicators for galaxies is the Type Ia Supernova. A Type Ia supernova occurs when a white dwarf in a binary system funnels material off of its binary companion, causing it to gain mass until eventually it exceeds the Chandrasekhar limit of 1.4 solar masses. At this mass limit, the white dwarf's electron degeneracy pressure can no longer balance the inward force of gravity, and the white dwarf explodes. Because all white dwarfs explode at the same mass limit, their explosions are very similar, causing their light curves (a plot of light intensity as observed from Earth over time) to be remarkably similar as well. A typical light curve for a Type Ia supernova is shown below. Specifically, all Type Ia supernovae peak at around the same luminosity. Just observe a Type Ia supernova event at its peak of maximum emission, and it can be used as a distance indicator. Because Type Ia supernovae are so luminous, they can be observed at great distances, out to 1 Gpc, 1 billion parsecs away.

Light Curve for a type Ia supernova (http://www.cortinastelle.it/)

24.7 Standard Candles

Many of the objects we've featured in this activity are useful distance indicators because, at least at one point in their evolution, they have a well-known luminosity. We call objects like these standard candles. If you can observe a standard candle at the moment in its life when we know its luminosity and also determine its apparent brightness, then you can use the inverse square law of light to determine the distance to that object, as well as the galaxy in which it resides.

In order for a standard candle to be effective, it must satisfy a number of criteria. First, it should be luminous, so that it may be observed as far away as possible. Second, its luminosity must be very well known, at least at one point in its life, so that it may yield an accurate distance measurement. Third, it must be easy to observe. In other words, it can't look like every other star in the galaxy. It must stand out, either by how its light varies over time, or in some other manner. Finally, it should be common enough that we can find them in other galaxies so that we can measure their distances. Given all of these criteria, some standard candles can be used to measure distances much further away than the methods already discussed. Astronomers have found that the following objects can be used as standard candles: variable stars, eclipsing binaries, stars that lie in the tip of the red giant branch on the H-R diagram, planetary nebulae, globular star clusters, and X-ray bursters.

The animation above depicts three galaxies at various distances from Earth. Each one has a distance indicator present. Hover over each galaxy and see happens and how astronomers can determine each galaxy's distance.

24.8 Uncertainty Grows with Distance

A problem arises when using these various techniques to measure distances to galaxies very far away. In general, the greater the distance to an object, the more uncertainty there is in the measurement. The reason is that the accuracy of a distant measurement depends on the accuracies of measurements to closer objects. For example, if you remember the story of Henrietta Leavitt, when she first studied Cepheid Variables in the Small Magellanic Cloud, she was only able to determine their apparent brightnesses, and compare those values to their periods of variation. How did astronomers determine their luminosities? To do so, they had to use another distance measurement technique (for example, spectroscopic parallax). Any uncertainty in this method would create an uncertainty in the measured distances to the Cepheid variables used to calculate their luminosities, which in turn would create an uncertainty in the period-luminosity relationship.

How did Tully & Fisher determine the luminosities of galaxies in order to correlate this value with their rotation rates? They knew the distances to nearby galaxies, which were determined using observations of Cepheid variables and in some cases Type Ia supernovae. Any uncertainty in these measurements created an uncertainty in the Tully-Fisher relation.

24.9 Quick Check Quiz

Indepth Activity: The Distance Ladder