LAND AND PHYSICAL CAPITAL
316
In the previous chapter, we discussed the importance of labor in the production process. But certainly more is required than just workers to run a business and produce products. A business also needs land and physical capital.
Land
rent The return to land as a factor of production. Sometimes called economic rent.
For economists, the term land includes both land in the usual sense and other natural resources that are inelastically supplied. Rent, sometimes called economic rent, is any return or income that flows to land as a factor of production. This is a different meaning from when we speak of the rent on an apartment. Land is unique among the factors of production because of its inelasticity of supply.
In some instances, the supply of land is perfectly inelastic. Finding an empty lot on which to build in San Francisco is virtually impossible. The land available is fixed by the terrain; it cannot be added to nor moved from one place to another.
Figure 1 shows how rent is determined when the available supply of land is fixed. In this example, the number of acres of usable land is fixed at L0 (or supply S0). If the demand for land is D0, the economic rent will be r0 (point a). When demand rises to D1, rent increases to r1 (point b). Notice that because the supply of land in this example is perfectly inelastic, rent depends entirely on demand. If demand were to fall, rent would fall as well.

In a strict sense, land is not perfectly fixed in supply. Land can be improved. Land that is arid, like the deserts of Arizona, can be improved through irrigation. Jungles can be cleared, swamps can be drained, and mountains can be terraced, making land that was once worthless productive.
Even more ambitious are cities that have reclaimed land in the ocean by extending out from the coastline or creating new islands using large amounts of sand. Balboa Island off Newport Beach, California, and Star Island off Miami Beach, Florida, are examples of artificially made islands. Much larger projects are seen in Asia, where land is limited due to large populations and mountainous terrain. Still, even if the supply of land is not perfectly inelastic, it is quite inelastic when compared to other production inputs.
The price of land varies based on many factors, such as its terrain, its view, but most importantly, its location. Why are land prices so much higher in Manhattan and San Francisco than in Iowa? Land prices are driven by demand from households and firms choosing to build a home or a business. Because the supply of land in any single location is fixed (or the least inflexible), changes in demand will cause large variations in land prices between more desirable and less desirable locations. But what determines a household or a firm’s desire to locate in a particular place? The cost of land is an obvious factor, but other factors also influence a firm’s potential profitability. For example, a business generally prefers to be close to its product market or its input suppliers.
317

Industrial agglomeration describes the geographical clusters of firms within an industry that choose to locate in close proximity with one another, such as Silicon Valley for the computer industry, Detroit for the auto industry, Dalton, Georgia, for the carpet industry, and Hollywood for the entertainment industry. By doing so, these firms benefit from external economies of scale. In a similar way, people of similar cultures sometimes choose to live near one another as well, leading to Chinatowns, Koreatowns, and Brazilian communities in various metropolitan areas throughout the country. Any time people choose a particular location for their home or business, demand for the land in that area increases, which will affect prices.
Physical Capital
physical capital All manufactured products that are used to produce goods and services.
Capital is the other important physical input in production. Physical capital includes all manufactured products that are used to produce goods and services. Examples of physical capital range from the massive cranes used to construct new skyscrapers to the espresso machine Starbucks uses to make your daily latte. Firms must determine what capital inputs are needed, and then calculate the value of adding additional capital to their production. When firms purchase capital inputs, it is called investment. The investment decisions by firms involve calculating the marginal benefits and costs of each capital input.
In the previous chapter, we introduced the concept of the marginal revenue product of labor (MRPL) and showed how firms choose to add additional units of labor if the cost of labor, or wage (W), is less than the MRPL. In the capital market, we study a similar concept called the marginal revenue product of capital (MRPK). Like MRPL, MRPK is downward-
When firms choose which capital inputs in which to invest, they clearly would make their most productive investments first. For a fast-
318
The cost of capital is the price of an additional unit of capital. Because the price of actual capital inputs varies significantly, we simplify things by measuring the cost of capital by its opportunity cost, or interest rate (i). In other words, to buy another capital input, firms must either borrow money and pay interest, or use savings and forgo interest. Thus, the interest rate can be used to measure the cost of capital.
Financial resources to pay for capital inputs come from the savings of households and other firms. Suppliers of funds and the demanders of these funds interact through what is called the loanable funds market. As with competitive labor markets, in which the market determines wages and each individual firm determines how many workers to employ, the loanable funds market determines interest rates, leaving individual firms to calculate how much they should borrow.
Through their interactions in the loanable funds market, suppliers and demanders determine the interest rates to be charged for funds. Individual firms then evaluate their investment opportunities to determine their own investment levels. Figure 2 shows how this process works. The demand and supply of loanable funds are shown in panel A, where equilibrium interest rates equal i0. Note that the demand for loanable funds looks just like a normal demand curve. Its downward slope shows that, as the price of funds declines—
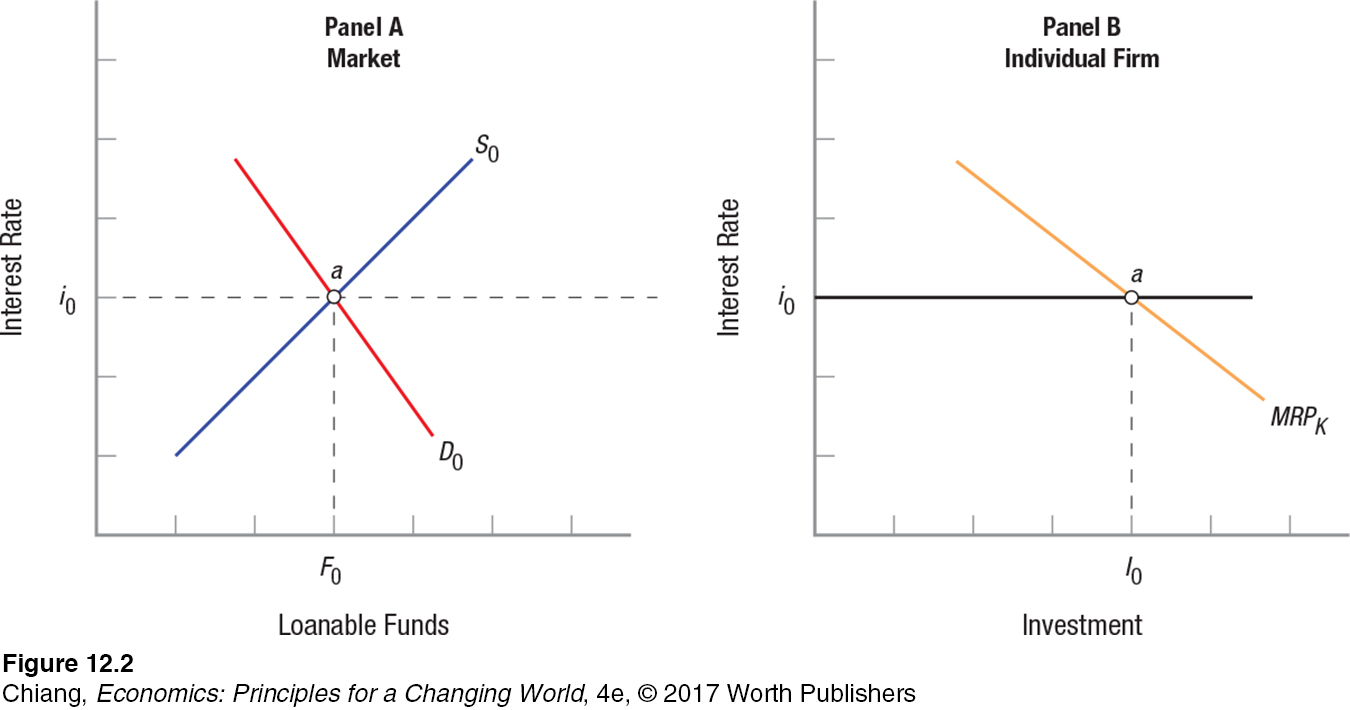
Once the market has determined an equilibrium rate of interest, an individual firm like the one shown in panel B will take this rate of interest, or cost of capital, and determine how much to invest.
This admittedly simplifies the investment process, but it is a good general model of investment decisions. Next, we turn to two more precise ways in which investment is determined, the present value approach and the rate of return approach.
Present Value Approach
319
present value The value of an investment (future stream of income) today. The higher the discount rate, the lower the present value today, and vice versa.
When a firm considers upgrading its information system or purchasing a new piece of equipment, a building, or a manufacturing plant, it must evaluate the returns it can expect over time. Firms invest money today, but earn returns over years. To compare investments having different income streams and different levels of required investment, firms look at the net present value of the investment.
The sum of $100 a year from now is worth less than $100 today. This is illustrated by the fact that you could put less than $100 in the bank today, earn interest on this money over the next year, and still end up with $100 at year’s end. Yet, exactly how much less than $100 would you be willing to give up today for $100 received a year from today? To answer this question, let us begin by looking at a simple form of financial assets, annuities.
An annuity is a financial instrument that pays the bearer a certain dollar amount in perpetuity, or generally for the life of the annuity holder. Assume that the market rate of interest is 5%, and you are offered an annuity that pays you or the holder of the annuity $1,000 a year indefinitely. How much would you be willing to pay for this annuity? If you want to follow the market in earning 5% a year, then the question you must ask is this: On what amount of money does $1,000 a year in income represent a 5% return? The answer is found through the formula:
PV = X/i
where PV is the present value of the investment (what you are willing to pay for the annuity today), X is the annual income ($1,000 in this case), and i is the market interest rate. In this case, you would be willing to pay $20,000 for this annuity, since $20,000 = $1,000/0.05. We have thus reduced an infinite stream of income to the finite amount you would pay today. You would pay $20,000, and the annuity would give you $1,000 a year, for an annual return on your investment of 5%.
What happens to the value of this annuity if the market interest rate should rise to 10%? You will still receive $1,000 a year, but if you want to sell the annuity to someone else, the buyer will only be willing to pay $10,000 for it ($10,000 = $1,000/0.10). Interest rates doubled, and the value of your annuity has been halved. Higher interest rates mean that income in future years is not worth as much today.
Valuing future income today by this process is known as discounting. This principle applies not only to annuities, but computing for years less than perpetuity requires a more complex formula. For example, assume that someone agrees to pay you $500 in two years as a gift upon your graduation, and that the going interest rate is 5%. What would you be willing to accept today instead of having to wait two years (assuming that you still will graduate)? The answer is found using the following formula:
PV = X/(1 + i)n
Again, PV is the present value of the future payment, X is the future payment of $500, i is the interest rate (5%), and n is the number of years into the future before the payment is made. In this case, the calculations are
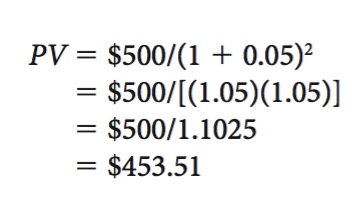
Hence, you would be willing to accept only $453.51 for this $500 payment coming two years in the future. Again, the higher the interest or discount rate, the lower the present value.
320
When only one future payment is at stake, computing the present value of that payment is fairly simple. When future streams of income are involved, however, things get more complicated. We must compute the present value of each individual future payment. The general formula looks nearly the same as before:
PV = ΣXn/(1 + i)n
Here, the Greek letter Σ (sigma) stands for “sum of,” and Xn is the individual payment received at year n. Assume, then, that you are going to receive $500, $800, and $1,200 over the next three years, and that the interest rate is still 5%. The present value of this income stream is therefore
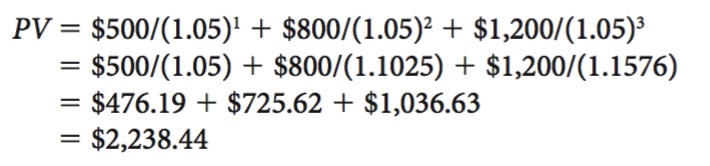
Given the complexity of such computations, economists often use computers to solve for present value, especially when the annual income stream is complicated. When the annual income is constant, tables of discount factors are also available. In any case, the point to note is that payments to be made in the future are worth a lower dollar amount today.
Firms often use present value analysis to determine if potential investments are worthwhile. Turning back to our chapter opener, suppose that an airline is considering installing broadband Internet access in all of its planes. Assume that the service will yield a stream of income (from charging users a fee) exceeding operating costs over a given period. The present value of this income is then compared to the cost of installing the Internet service. The service’s net present value (NPV) is equal to the difference between the present value of the income stream and the cost of installing the service. If NPV is positive, the firm will invest; if it is negative, the firm will choose not to invest.
When interest rates are high, firms will find fewer investment opportunities where NPV is positive because the higher discount rate reduces the value of the income streams for investments. As interest rates fall, more investment is undertaken by firms.
Rate of Return Approach
rate of return Uses the present value formula, but subtracts costs, then finds the interest rate (discount rate) at which this investment would break even.
An alternative approach to determining whether an investment is worthwhile involves computing the investment’s rate of return. This rate of return is also known as a firm’s marginal efficiency of capital, or its internal rate of return.
Computing an investment’s rate of return requires using essentially the same present value formula for income streams introduced previously with a slight modification: You have to explicitly consider the cost of capital in the calculation. This new formula is
PV = [ΣXn/(1 + i)n] − C
where C represents the cost of capital. The question we must ask is: At what rate of interest (i) will the investment just break even? You would compute the present value of the income streams, then subtract the cost of the capital investment, and finally find the rate of interest (i) where the present value equals zero. This discount rate is the rate of return on the investment.
Suppose you find a rare vintage car for sale at $20,000 that you believe will be worth $25,000 next year. If you buy this car with the intention of selling it next year, the rate of return that would allow your investment to break even would be calculated as
0 = [$25,000/(1 + i)1] − $20,000
Solving for i yields a rate of return of 25%.
321
The calculated rate of return can be compared to the firm’s required rate of return on investments to determine whether the investment is worthwhile. The firm might require, say, a 20% yield on all projects based on the opportunity cost of the investment, in which case investments yielding returns of less than 20% are deemed not worthwhile. Risk in investment projects is usually managed by adding a risk premium to the required rate of return for risky projects. This risk premium can vary by project type or with the business cycle. Some investments, such as drilling for oil or researching innovative new drugs, are risky and require high rates of return if they are to be undertaken.
CHECKPOINT
LAND AND PHYSICAL CAPITAL
Land includes both land and natural resources and is inelastically supplied. Returns on land are called rents (or economic rent).
Because land is inelastically supplied, the rent on land is determined by demand.
Firms weigh the benefits of investing in physical capital such as new buildings or machinery versus their costs.
To compare investments with different investment streams over time, firms will use either the present value approach or the rate of return approach.
QUESTION: Suppose a good friend asks you to invest in some new equipment for her smoothie shop on campus in exchange for a share of the income earned at the end of the year. It will cost $10,000 to lease the new equipment for one year. What type of data and information would you be interested in estimating before you decide whether to pursue this investment?
Answers to the Checkpoint questions can be found at the end of this chapter.
To determine whether this investment is worthwhile, you would want to know how much income the store expects to generate over the year, as well as the current market interest rate. Using this information, you can estimate the net present value of the investment to determine whether it is a good idea or not. The higher the market interest rate, the greater the income stream you would require to invest.