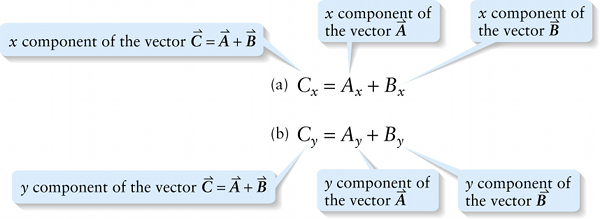
Rules for vector addition using components (3-3)

Balloon Art Concept Check: Click on the part of the equation that is described by the bubble text shown

Question 1 of 6

Question

\(x\) component of the vector \(\boldsymbol{\vec{B}}\)
Feedback
{"title":"x component of the vector C = A + B","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"rect\",\"coords\":\"58,5,89,40\"}]"} {"title":"x component of the vector A","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"157,1,197,39\"}]"} {"title":"x component of the vector B","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"254,5,283,41\"}]"} {"title":"y component of the vector C = A + B","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"55,112,107,157\"}]"} {"title":"y component of the vector A","description":"Incorrect","type":"incorrect","color":"#333333","code":"[{\"shape\":\"rect\",\"coords\":\"158,111,192,155\"}]"} {"title":"y component of the vector B","description":"Incorrect","type":"incorrect","color":"#800000","code":"[{\"shape\":\"rect\",\"coords\":\"247,111,288,159\"}]"}

Review

Describing vectors in terms of their components greatly simplifies the vector arithmetic that we described in Section 3-2. Here are the rules: If you add the vectors \(\vec{A}\) and \(\vec{B}\) to form the vector sum \(\vec{C} = \vec{A} + \vec{B}\), each component of \(\vec{C}\) is just the sum of the corresponding components of \(\vec{A}\) and \(\vec{B}\).