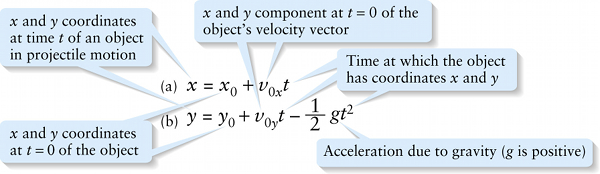
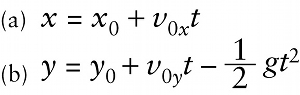Chapter 3. Position, acceleration, and time for projectile motion (3-13)

Review

We can use another equation from Chapter 2 to write down the equations for the projectile’s \(x\) and \(y\) coordinates \(x\) and \(y\) at any time \(t\). We let \(x\) and \(y\) be the projectile’s coordinates at time \(t=0\). Because the \(x\) component of acceleration \(a_x\) is constant, we know that \(x = x_0 + v_{0x}t + (1/2)a_xt^2\) from Equation 2-10 in Section 2-5. The same equation rewritten for the \(y\) direction is \(y=y_0 + v_{0y}t + (1/2)a_yt^2\). For projectile motion \(a_x = 0\) and \(a_y = -g\), so these equations become: