Chapter 6. Speed, acceleration, and position for stright-line motion with constant acceleration (6-4)

Question

E5ANxZhYQmO9/PzTiEj5vn40fcRcBJsvBLOq4qpyvJL/ABBGLhgV9FoEcKkR0ozwwwW8aSqIlAE2r4Tqn3gj+wgfnqRDcY/qUGIhhoswDN0YJ+pOdW39n7/Hh4RHWQg3uqQUuQ==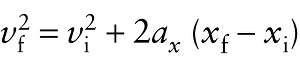

{"title":"Speed at position x sub f of an object in linear motion with constant acceleration","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"1,26,21,47\"}]"} {"title":"Speed at position x sub i of the object","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"66,23,83,45\"}]"} {"title":"Two positions of the object","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"264,23,284,49\"},{\"shape\":\"rect\",\"coords\":\"198,21,219,49\"}]"} {"title":"Constant acceleration of the object","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"150,23,171,49\"}]"}

Question

RjToufUJPxqGv2tQPpoF+oSBUn+ENxIbb85k9v/6o3X8JSzGo/x4RcgCT7mfjz1UPMiAgY/9lxs=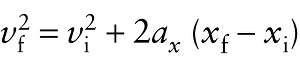

{"title":"Speed at position x sub f of an object in linear motion with constant acceleration","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"1,26,21,47\"}]"} {"title":"Speed at position x sub i of the object","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"66,23,83,45\"}]"} {"title":"Two positions of the object","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"264,23,284,49\"},{\"shape\":\"rect\",\"coords\":\"198,21,219,49\"}]"} {"title":"Constant acceleration of the object","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"150,23,171,49\"}]"}

Question

Uq+BIWr/DJpLO1VXIuhTyV7eXVMtrHguBZSRSv0I6RI=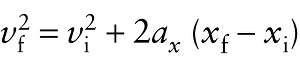

{"title":"Speed at position x sub f of an object in linear motion with constant acceleration","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"1,26,21,47\"}]"} {"title":"Speed at position x sub i of the object","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"66,23,83,45\"}]"} {"title":"Two positions of the object","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"264,23,284,49\"},{\"shape\":\"rect\",\"coords\":\"198,21,219,49\"}]"} {"title":"Constant acceleration of the object","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"150,23,171,49\"}]"}

Question

PkaxFVWjhURWwg9qPHARf9sZc6sDrC0DItLK1xaLPZ5rtK6Es6oU+Q==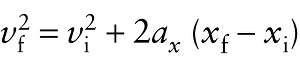

{"title":"Speed at position x sub f of an object in linear motion with constant acceleration","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"1,26,21,47\"}]"} {"title":"Speed at position x sub i of the object","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"66,23,83,45\"}]"} {"title":"Two positions of the object","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"264,23,284,49\"},{\"shape\":\"rect\",\"coords\":\"198,21,219,49\"}]"} {"title":"Constant acceleration of the object","description":"Correct!","type":"correct","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"150,23,171,49\"}]"}

Review

In Equation 6-3 \(v_{fx}^2\) is the square of the velocity at \(x_f\), but it also equals the square of the object’s \(\textit{speed}\) \(v_f\) at \(x_f\). That’s because \(v_{fx}\) is equal to \(+v_f\) if the object is moving in the positive \(x\) direction and equal to \(-v_f\) if moving in the negative \(x\) direction. In either case,\(v_{fx}^2 = v_{f}^2\) . For the same reason \(v_{ix}^2\) = \(v_{i}^2\) , where \(v_i\) is the object’s speed at \(x_i\). So we can rewrite Equation 6-3 as: