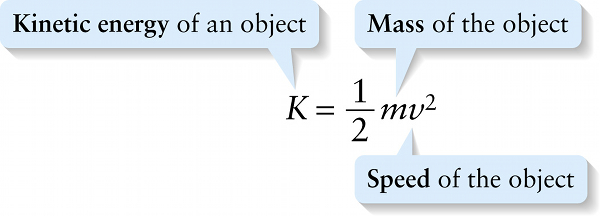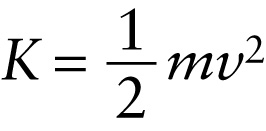Kinetic energy (6-8)

Balloon Art Concept Check: Click on the part of the equation that is described by the bubble text shown

Question 1 of 3

Question

\(\textbf{Speed}\) of the object
Feedback
{"title":"Kinetic energy of an object","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"2,32,42,83\"}]"} {"title":"Mass of the object","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"165,46,214,82\"}]"} {"title":"Speed of the object","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"215,46,245,79\"}]"}

Review

The right-hand side of Equation 6-7 is the \(\textit{change}\) in the quantity \(\frac{1}{2}mv^2\) over the course of the displacement (the value at the end of the displacement, where the speed is \(v_f\), minus the value at the beginning where the speed is \(v_i\)). We call this quantity the kinetic energy \(K\) of the object: