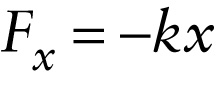Hooke's law (6-11)

Balloon Art Concept Check: Click on the part of the equation that is described by the bubble text shown

Question 1 of 3

Question

\(\textbf{Spring constant}\) of the spring (a measure of its stiffness)
Feedback
{"title":"Force exerted by an ideal spring","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"1,3,35,54\"}]"} {"title":"Spring constant of the spring (a measure of its stiffness)","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"152,7,183,50\"}]"} {"title":"Extension of the spring (x > 0 if spring is stretched, x < 0 if spring is compressed","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"183,17,213,56\"}]"}

Review

Experiment shows that if you stretch a spring by a relatively small amount, the force that the spring exerts on you is directly proportional to the amount of stretch (Figure 6-17). We can write this relationship, known as Hooke’s law, as \(F_x = -kx\).

The minus sign in Equation 6-11 means that the force that the spring exerts on you is in the direction opposite to the stretch.