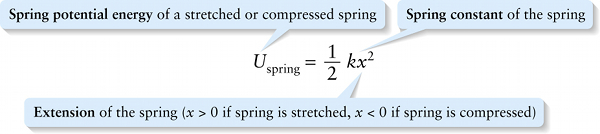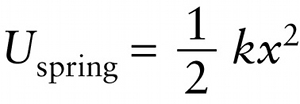Chapter 12. Spring potential energy (6-19)

Question

6Cx2FgDNqytaVM5321oskxOn8hgdULAKG2IUOVcCclDQbmsiiXicKMO3sJQkeEHBgpWH2bdgEcZuxWoxrRPpZd0WZDdY/O1//U/rMg==

{"title":"Spring potential energy of a stretched or compressed spring","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"4,25,34,62\"}]"} {"title":"Spring constant of the spring","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"234,22,258,64\"}]"} {"title":"Extension of the spring (x > 0 if spring is stretched, x < 0 if spring is compressed)","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"260,39,280,65\"}]"}

Question

EsXBRaX7Xtf0H4QpkPnAl+6gkd67ra6xWnOxnXclgif2Zbpfq1AoTi3DzMgDooXk

{"title":"Spring potential energy of a stretched or compressed spring","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"4,25,34,62\"}]"} {"title":"Spring constant of the spring","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"234,22,258,64\"}]"} {"title":"Extension of the spring (x > 0 if spring is stretched, x < 0 if spring is compressed)","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"260,39,280,65\"}]"}

Question

w+3NcIJzTF4gY0aU4K89xAXfeMz7ws5Hy7OUXgY7a1RqhRUE5rsy40kfMn4ymY+T4G1vxu3gI40iblF0M/+6zvI+58yTlTXl+NrSg68CjIASSY/ugB7nYKR5KFwZwSRx

{"title":"Spring potential energy of a stretched or compressed spring","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"4,25,34,62\"}]"} {"title":"Spring constant of the spring","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"234,22,258,64\"}]"} {"title":"Extension of the spring (x > 0 if spring is stretched, x < 0 if spring is compressed)","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"260,39,280,65\"}]"}

Review

It’s worthwhile to look at oscillations again from an energy perspective. To do this, we’ll study the interplay between kinetic energy and potential energy for a block connected to the free end of an ideal, Hooke’s law spring, oriented horizontally as in Figures 12-2 and 12-3.

Our starting point is the expression from Section 6-6 for the potential energy stored in an ideal spring: