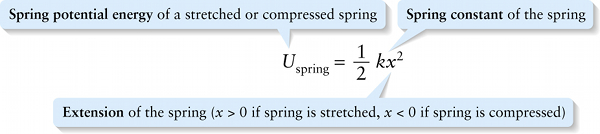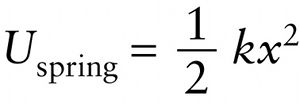Spring potential energy (6-19)

Balloon Art Concept Check: Click on the part of the equation that is described by the bubble text shown

Question 1 of 3

Question

Spring constant of the spring
Feedback
{"title":"Spring potential energy of a stretched or compressed spring","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"2,24,38,66\"}]"} {"title":"Spring constant of the spring","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"232,21,257,67\"}]"} {"title":"Extension of the spring (x > 0 if spring is stretched, x < 0 if spring is compressed)","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"258,39,283,65\"}]"}

Review

The only differences between \(U_{\mathrm{electric}} = q^2/(2C)\) from Equation 17-17 and the expression in Equation 6-19 is that the spring displacement \(x\) is replaced by the charge \(q\) and the spring constant \(k\) is replaced by the reciprocal of the capacitance, \(1/C\). This similarity isn’t surprising. To add potential energy to a spring by stretching it, you have to pull against the force of magnitude \(F = kx\) that the spring exerts on you. The greater the distance that the spring is already stretched, the more force it exerts and the harder it is to stretch it further.