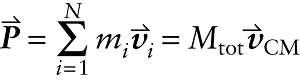Total momentum and the velocity of the center of mass (7-33)
Question 1 of 3
Question
The total momentum of a system...
{"title":"The total momentum of a system...","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"1,8,20,52\"}]"} {"title":"... equals the vector sum of the momentum of all objects in the system...","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"130,25,151,52\"}]"} {"title":"... and also equals the total mass of the system multiplied by the velocity of the center of mass.","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"217,39,249,60\"}]"}Review
The quantity \(m_i\vec{v}_i\) on the right-hand side of Equation 7-32 should be familiar: This is just the momentum of the \(i\)th object in the system. So \(\sum_{i=1}^N m_i\vec{v}_i\) is the vector sum of the momentum of all objects that make up the system. This is just the \(\textit{total}\) momentum of the system, which we denote as \(\vec{P}\). If we multiply Equation 7-32 by the total mass of the system \(M_\mathrm{tot}\), we get