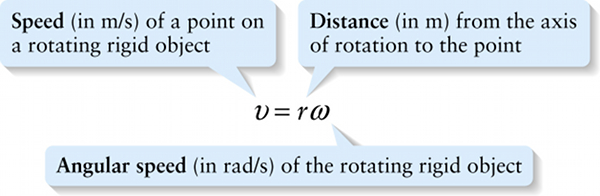
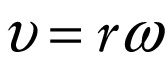Speed of a point on a rotating rigid object (8-3)

Balloon Art Concept Check: Click on the part of the equation that is described by the bubble text shown

Question 1 of 3

Question

\(\textbf{Speed}\) (in m/s) of a point on a rotating rigid object
Feedback
{"title":"Speed (in m/s) of a point on a rotating rigid object","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"3,21,42,56\"}]"} {"title":"Distance (in m) from the axis of rotation to the point","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"91,20,122,54\"}]"} {"title":"Angular speed (in rad/s) of the rotating rigid object","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"128,18,165,54\"}]"}

Review

\(\Delta{\theta}/\Delta{t}\) is the angular speed \(\omega\) of a rotating blade. (Since the blade is rotating in the positive direction, its angular velocity \(\omega_z = \Delta{\theta}/\Delta{t}\) is positive and so the angular speed \(\omega\)—which is always positive—is the same as \(\omega_z\).) So we can rewrite Equation 8-2 for the speed of a point on the blade as