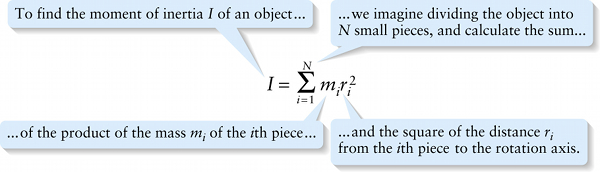
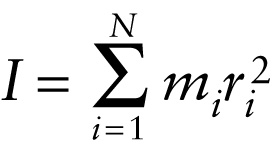Moment of inertia of an object (8-6)
Question
...and the square of the distance \(r_i\) from the \(i\)th piece to the rotation axis.
{"title":"To find the moment of inertia \\(I\\) of an object...","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"2,53,25,103\"}]"} {"title":"...we imagine dividing the object into N small pieces, and calculate the sum...","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"109,7,140,41\"}]"} {"title":"...of the product of the mass m sub i of the ith piece...","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"161,68,211,104\"}]"} {"title":"...and the square of the distance r sub i from the ith piece to the rotation axis.","description":"Correct!","type":"correct","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"220,67,250,106\"}]"}Review
What is the quantity in parentheses in Equation 8-5, \(\sum_{i=1}^Nm_i r_i^2\)? Although it involves a sum over all the little pieces into which we’ve divided the turbine blade, it is \(\textit{not}\) simply the total mass \(M\) of the blade. That sum would be \(M = \sum_{i=1}^Nm_i\), without the factor of \(r_i^2\). Instead, the sum \(\sum_{i=1}^Nm_i r_i^2\) is a new quantity that tells us how the mass of the blade is \(\textit{distributed:}\) It depends on both the mass of each small piece \(m_i\) and how far away from the rotation axis that piece is (\(r_i\)). This quantity is called the \(\textbf{moment of inertia}\) (sometimes called \(\textit{rotational inertia}\)) of the turbine blade. We represent it by the symol \(I\):