Chapter 8. Total kinetic energy for a rigid object undergoing both translation and rotation (8-12)

Question

dt2MPvt/Es8XB9fsw8Vx73sLP1mlC4W78qUIIhNvKYdFS4YPoVbnCRwxCWZcHwXaQHjBmQmEGffv2Q1mXzHLmEW2vXSOLD3VU1MZDw==

{"title":"1) Total kinetic energy of a system that is both translating and rotating","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"2,6,17,25\"}]"} {"title":"2) The translational kinetic energy is the same as if all of the mass of the system were moving at the speed of the center of mass.","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"25,5,43,25\"},{\"shape\":\"rect\",\"coords\":\"187,6,205,25\"}]"} {"title":"3) The rotational kinetic energy is the same as if the system were not translating, and all of the mass were rotating around the center of mass.","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"112,13,161,29\"},{\"shape\":\"rect\",\"coords\":\"268,15,290,30\"}]"}

Question

4vRNhzNZ/GITt+BZn/Xjpto6x8hDsfSFE15e3iaIdoTvcBX53CWcMJeRhC4TI8gL4FevEnRxLzlkDPlXyX33rjyoJO6LQmSoSu6jeaF/sx06+FLmRIkKzWRsEtwhzPwdqHuezR9Wi1oewk2VEZ5zEKTsHM2kxfmLoB9LCpKf6R00cDMW

{"title":"1) Total kinetic energy of a system that is both translating and rotating","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"2,6,17,25\"}]"} {"title":"2) The translational kinetic energy is the same as if all of the mass of the system were moving at the speed of the center of mass.","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"25,5,43,25\"},{\"shape\":\"rect\",\"coords\":\"187,6,205,25\"}]"} {"title":"3) The rotational kinetic energy is the same as if the system were not translating, and all of the mass were rotating around the center of mass.","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"112,13,161,29\"},{\"shape\":\"rect\",\"coords\":\"268,15,290,30\"}]"}

Question

XgL36gSKpIwG4Gp52+13xeSCRGk+H4pyuriUrDt4E3qDRfG13oQ2YbjcEVLyuDuaRMoiq4tLks2qEZkZ7w1PZcjDx8G0gCoUZvM8nQ5k26boJ0eP+/dy8B67zq9sArsnHT6Zy+rg4ASeVnCayoE8kgQZcuxHVj68/ZLwJ/b3nuIs8AiFT3cswRHMVbihEm8PTL6YSw==

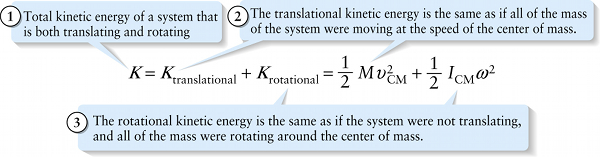
{"title":"1) Total kinetic energy of a system that is both translating and rotating","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"2,6,17,25\"}]"} {"title":"2) The translational kinetic energy is the same as if all of the mass of the system were moving at the speed of the center of mass.","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"25,5,43,25\"},{\"shape\":\"rect\",\"coords\":\"187,6,205,25\"}]"} {"title":"3) The rotational kinetic energy is the same as if the system were not translating, and all of the mass were rotating around the center of mass.","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"112,13,161,29\"},{\"shape\":\"rect\",\"coords\":\"268,15,290,30\"}]"}

Review

We can also use the principle of conservation of energy for a rigid object that’s both moving through space as a whole and rotating. In such a situation it turns out that we can write the object’s \(\textit{total}\) kinetic energy as the sum of two terms: the \(\textit{translational}\) kinetic energy associated with the motion of the object’s center of mass (see Section 7-7), and the \(\textit{rotational}\) kinetic energy associated with the object’s rotation around its center of mass (Figure 8-12). If the object has mass \(M\) and its center of mass is moving with speed \(v_\mathrm{CM}\), its translational kinetic energy is \(K = \frac{1}{2}Mv_\mathrm{CM}^2\) ; if the object’s moment of inertia for an axis through its center of mass is \(I_\mathrm{CM}\) and it rotates with angular speed \(\omega\), its rotational kinetic energy is \(K_\mathrm{rotational} = \frac{1}{2}I_\mathrm{CM}\omega^2\). The total kinetic energy (translational plus rotational) of the object is then: