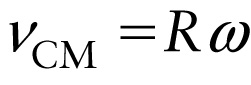Condition for rolling without slipping (8-13)

Balloon Art Concept Check: Click on the part of the equation that is described by the bubble text shown

Question 1 of 3

Question

\(\textbf{Angular speed}\) of the object’s rotation
Feedback
{"title":"Speed of the center of mass of a rolling object","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"6,18,38,52\"}]"} {"title":"Radius of the object","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"168,9,198,55\"}]"} {"title":"Angular speed of the object’s rotation","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"210,18,250,56\"}]"}

Review

Equation 8-13 says that there is a direct proportionality between the linear speed \(v_\mathrm{CM}\) and angular speed \(\omega\) of a circular object that rolls without slipping. As the wheel in Figure 8-13 rolls downhill it gains speed so \(v_\mathrm{CM}\) increases, and it rotates faster so \(\omega\) increases, but these increases are always proportional to each \perpher so that \(v_\mathrm{CM}\) and \(\omega\) are always related by Equation 8-13.