Chapter 8. Angular velocity, angular acceleration, and time for constant angular acceleration only (8-15)
Question
YUTcR8i8aEsQI7cEy+gI6dhoQ8eT4eT5yWiB1M49PlaZPD7yPcACmNmSEjpsXgf/DFB/XGx4vkFCXA6z09YnRaR43SeN+qdL/XZgDGo+S/L/sMlb6eRTuB1c745PoYdjEi53Qg==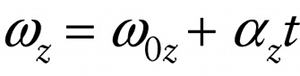
Question
H1GzuBM5OJY9dlHmf/dmlA9woSRRoguH81sDsZbH2nE/LKd1V5DhZbY7aMigNjY85uNlQUZmCV6AMetHDXlEquc7t/s=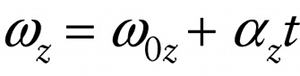
Question
R6NVI2/fQ0KohlQ0t/WeafImF1x35FX6BngvkGu5VEbQQVnPESDroW2U/i/P0cozQ9YoqPuB7HdmxjbY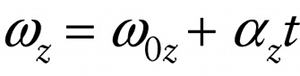
Question
I+auTfQEELiQTtLLhh5lhkRtA0NZgcEe2t5cdu5D2hqiBLGG69eWP7xuuuZE8O6nOgh1Xz8hxfWK2jUpwE7LWPKW4shIHRFqqs0/CA==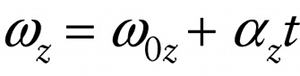
Review
It’s straightforward to write down the equations for rotational motion with constant angular acceleration. To see how, take a look at the equations for linear velocity \(v_x\) and angular velocity \(\omega_z\), and the equations for linear acceleration \(a_x\) and angular acceleration \(\alpha_z\):
| Linear Motion | Rotational Motion | ||
|---|---|---|---|
|
|
(linear velocity) |
|
(angular velocity) |
|
|
(linear acceleration) |
|
(angular acceleration) |
Comparing these equations shows that the rotational quantities \(\theta\), \(\omega_z\), and \(\alpha_z\) are related to each \perpher in exactly the same way that \(x\), \(v_x\), and \(a_x\) are related to each \perpher. So we can take the equations for constant linear acceleration and convert them to the equations for constant angular acceleration by replacing \(x\) with \(\theta\), \(v_x\) with \(\omega_z\), and \(a_x\) with \(\alpha_z\). The equations for linear motion are:
(2-5) \(v_x = v_{0x} + a_xt\) (constant acceleration only)
(2-9) \(x = x_0 + v_{0x}t + \frac{1}{2}a_xt^2\) (constant \(x\) acceleration only)
(2-11) \(v_x^2 = v_{0x}^2 + 2a_x(x - x_0)\) (constant \(x\) acceleration only)
Hence, along with equation 8-16 and 8-17, the equation for constant angular acceleration is:
