Angular position, angular acceleration, and time for constant angular acceleration only (8-16)

Question 1 of 5

Question

$\textbf{Constant angular acceleration}$ of the object

{"title":"Angular position at time t of a rotating object with constant angular acceleration","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"4,19,23,51\"}]"} {"title":"Angular velocity at time t = 0 of the object","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"119,21,143,47\"}]"} {"title":"Constant angular acceleration of the object","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"243,24,271,50\"}]"} {"title":"Angular position at time t = 0 of the object","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"58,20,76,51\"}]"} {"title":"Time at which the object is at angular position theta","description":"Incorrect","type":"incorrect","color":"#333333","code":"[{\"shape\":\"rect\",\"coords\":\"157,23,175,50\"},{\"shape\":\"rect\",\"coords\":\"273,26,290,49\"}]"}

Question

$\textbf{Angular position}$ at time $t$ of a rotating object with constant angular acceleration

{"title":"Angular position at time t of a rotating object with constant angular acceleration","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"4,19,23,51\"}]"} {"title":"Angular velocity at time t = 0 of the object","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"119,21,143,47\"}]"} {"title":"Constant angular acceleration of the object","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"243,24,271,50\"}]"} {"title":"Angular position at time t = 0 of the object","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"58,20,76,51\"}]"} {"title":"Time at which the object is at angular position theta","description":"Incorrect","type":"incorrect","color":"#333333","code":"[{\"shape\":\"rect\",\"coords\":\"157,23,175,50\"},{\"shape\":\"rect\",\"coords\":\"273,26,290,49\"}]"}

Question

$\textbf{Angular velocity}$ at time $t = 0$ of the object

{"title":"Angular position at time t of a rotating object with constant angular acceleration","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"4,19,23,51\"}]"} {"title":"Angular velocity at time t = 0 of the object","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"119,21,143,47\"}]"} {"title":"Constant angular acceleration of the object","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"243,24,271,50\"}]"} {"title":"Angular position at time t = 0 of the object","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"58,20,76,51\"}]"} {"title":"Time at which the object is at angular position theta","description":"Incorrect","type":"incorrect","color":"#333333","code":"[{\"shape\":\"rect\",\"coords\":\"157,23,175,50\"},{\"shape\":\"rect\",\"coords\":\"273,26,290,49\"}]"}

Question

$\textbf{Angular position}$ at time $t = 0$ of the object

{"title":"Angular position at time t of a rotating object with constant angular acceleration","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"4,19,23,51\"}]"} {"title":"Angular velocity at time t = 0 of the object","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"119,21,143,47\"}]"} {"title":"Constant angular acceleration of the object","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"243,24,271,50\"}]"} {"title":"Angular position at time t = 0 of the object","description":"Correct!","type":"correct","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"58,20,76,51\"}]"} {"title":"Time at which the object is at angular position theta","description":"Incorrect","type":"incorrect","color":"#333333","code":"[{\"shape\":\"rect\",\"coords\":\"157,23,175,50\"},{\"shape\":\"rect\",\"coords\":\"273,26,290,49\"}]"}

Question

$\textbf{Time}$ at which the object is at angular position $\theta$

{"title":"Angular position at time t of a rotating object with constant angular acceleration","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"4,19,23,51\"}]"} {"title":"Angular velocity at time t = 0 of the object","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"119,21,143,47\"}]"} {"title":"Constant angular acceleration of the object","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"243,24,271,50\"}]"} {"title":"Angular position at time t = 0 of the object","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"58,20,76,51\"}]"} {"title":"Time at which the object is at angular position theta","description":"Correct!","type":"correct","color":"#333333","code":"[{\"shape\":\"rect\",\"coords\":\"157,23,175,50\"},{\"shape\":\"rect\",\"coords\":\"273,26,290,49\"}]"}

Review

It’s straightforward to write down the equations for rotational motion with constant angular acceleration. To see how, take a look at the equations for linear velocity $v_x$ and angular velocity $\omega_z$ , and the equations for linear acceleration $a_x$ and angular acceleration $\alpha_z$ :

Linear Motion		Rotational Motion
	(linear velocity)		(angular velocity)
	(linear acceleration)		(angular acceleration)

Table 8.1: Linear and Angular Motion

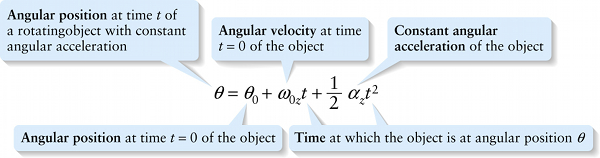
Comparing these equations shows that the rotational quantities $\theta$ , $\omega_z$ , and $\alpha_z$ are related to each \perpher in exactly the same way that $x$ , $v_x$ , and $a_x$ are related to each \perpher. So we can take the equations for constant linear acceleration and convert them to the equations for constant angular acceleration by replacing $x$ with $\theta$ , $v_x$ with $\omega_z$ , and $a_x$ with $\alpha_z$ . The equations for linear motion are:

(2-5) $v_x = v_{0x} + a_xt$ (constant acceleration only)

(2-9) $x = x_0 + v_{0x}t + \frac{1}{2}a_xt^2$ (constant $x$ acceleration only)

(2-11) $v_x^2 = v_{0x}^2 + 2a_x(x - x_0)$ (constant $x$ acceleration only)

Hence, along with equations 8-15 and 8-17, the equation for constant angular acceleration is: