Chapter 8. Magnitude of torque (8-18)
Question
47d8KkSDci1Rke3qAr2go2cY33X0vEELdE2Xc03NTgQyuPMIj8zq12jaHuv6rIkeTfkTVP2NLgAmIWVoAPFZidQQQ2uPLhhjHAFYBLUbFjY=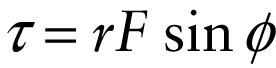
Question
Z340wLstWf6CxX+SFjdBxMeoJ2tXpWxDNB1A4g==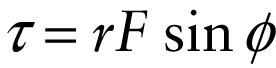
Question
QzgABDtqACV+YhEP3+TDulBd3YATA0Tr8n+wDmcytU7yekMqltl9acwK/h0toXozk0xdDbjuNO3Au+Opny+VzITxaG8PXGtUCjqAlY5B4AlA9N7pwU8DmiFyQok2S1b4Gao3fBTRPPYnT16/j+Wr6z28ERv8KYRMyPle0rk0Bo8=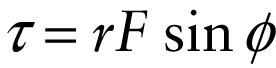
Question
VdH/jhPrNBjap1BBZphryIPeBq6R3UgAhg5sNoh22uBHtuCZFkGdAUjxPRlcnDAtesVWhaOQjLzhyPhvLB3+1ZeMbSJoZJQiPhiEKKR1Qlc=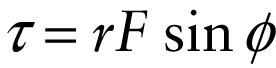
Review
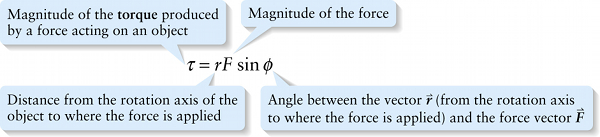
Suppose that you exert a force \(\vec{F}\) on an object as shown in Figure 8-19a. We use the symbol \(\vec{r}\) to denote the vector from the rotation axis to the point where the force is applied, and we use the symbol \(\phi\) (the Greek letter phi) for the angle between the directions of \(\vec{r}\) and \(\vec{F}\). The component of \(\vec{F}\) that points straight out from the rotation axis, \(F\ \mathrm{cos}\ \phi\), doesn’t have any tendency to make the object rotate. But the perpendicular component of \(\vec{F}\), \(F\ \mathrm{sin}\ \phi\), \(\textit{does}\) tend to make the object rotate—in this case in a clock-wise direction. We describe the rotational effect of the force \(\vec{F}\) by a quantity called the torque \(\tau\) (the Greek letter tau) associated with the force. This is given by: