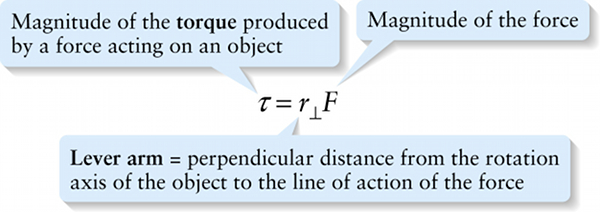
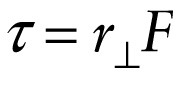Magnitude of torque in terms of lever arm (8-19)

Question 1 of 3

Question

$\textbf{Lever arm}$ = perpendicular distance from the rotation axis of the object to the line of action of the force

{"title":"Magnitude of the torque produced by a force acting on an object","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"4,19,40,53\"}]"} {"title":"Magnitude of the force","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"139,8,174,53\"}]"} {"title":"Lever arm = perpendicular distance from the rotation axis of the object to the line of action of the force","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"83,12,119,57\"}]"}

Question

Magnitude of the $\textbf{torque}$ produced by a force acting on an object

{"title":"Magnitude of the torque produced by a force acting on an object","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"4,19,40,53\"}]"} {"title":"Magnitude of the force","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"139,8,174,53\"}]"} {"title":"Lever arm = perpendicular distance from the rotation axis of the object to the line of action of the force","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"83,12,119,57\"}]"}

Review

Figure 8-19c shows another way to calculate the magnitude of the torque for the situation in Figure 8-19a. As this figure shows, the $\textbf{line of action}$ of the force is just an extension of the force vector $\vec{F}$ through the point where the force is applied. The $\textbf{lever arm}$ of the force (also called the $\textit{moment arm}$ ) is the perpendicular distance from the rotation axis to the line of action of the force, which is why we denote it by the symbol $r_\perp$ ( $\perp$ is mathematical shorthand for “perpendicular”). Trigonometry shows that the lever arm $r_\perp$ equals $r \sin{\phi}$ , the same quantity that appears in Equation 8-18. Hence we can rewrite that equation as: