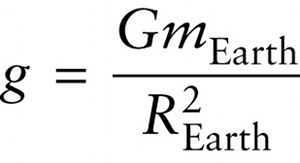Value of g at Earth's surface (10-3)

Balloon Art Concept Check: Click on the part of the equation that is described by the bubble text shown

Question 1 of 4

Question

Mass of Earth
Feedback
{"title":"Gravitational constant","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"117,5,155,46\"}]"} {"title":"Mass of Earth","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"163,15,204,46\"}]"} {"title":"Radius of Earth","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"poly\",\"coords\":\"113,132\"},{\"shape\":\"rect\",\"coords\":\"134,93,181,137\"}]"} {"title":"Acceleration due to gravity at Earth’s surface","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"1,60,41,105\"}]"}

Review

Example 10-2 shows that there is a connection between the value of \(g\) at Earth’s surface and the values of \(G\) and \(m_{\mathrm{Earth}}\), the gravitational constant and Earth’s mass. To see this more clearly, take the two expressions for the gravitational force on you and set them equal to each \perpher:

\(F_\mathrm{Earth\ on\ you} = m_\mathrm{you}g = \frac{G_{m_\mathrm{Earth}}m_\mathrm{you}}{R_{\mathrm{Earth}}^2}\)

Then divide both sides of the equation by your mass, \(m_{\mathrm{you}}\), to get an expression for \(g\):