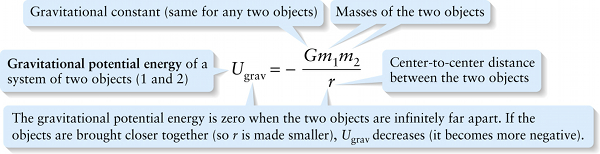
Chapter 10. Gravitation potential energy (10-4)
Question
YAedzCq0ZEOgMZeOeDspHoKP+DmzwlVk7RClNP60f6QuCE/8/krMzPawIDNhzlJk5WntdkR8J0c=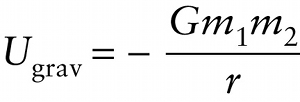
Question
tfDBnh/BepSwtrb1e/2zgz5IuSepnnA6sPKyVRXnm+k=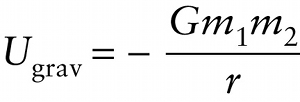
Question
LMP4MOB8r+d1yzLOdKTbwj8EPGomhMh072hoe+Pt4/SBRA8v+KTdcrL4JifJtIPqbbJ+CaI4CXo=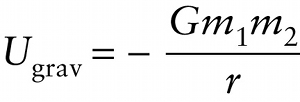
Question
/w8FK4or3P6Lj5Zb2QWGYHHlro+wyDBpYjPl6pUV0NW/iG6pOhLp1NVdU5mW6wm9Pa3m0I8Z06SnJhwAuCzZHsmFDFASE79BSRvvLGGe8WchyF1nQIbPX470+TJuLYn25Qa/rf3q3OUFyXRFfm6gZtvTydJGHZna2PN3aTPNQ4Fg0wFVL/mvoEhpCT5zXnGdfp+jd8VvBjKkFeAhYuODfN967oTxnVaJOnTmtH7QfPYk4MPHDPTuIaCDk7Vpi/PWnWU5fLL9e5mFux67uYHkQHZvz9fdhCOwdtUycRBcuic=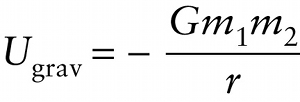
Question
US/z6SIbPRYmjtPx7ajlH+7vrmzUaEzBcjAHO/kd859ot39EOGTiNKSBbDJH3AKfGwBdfSAtmmm5YlSUvdkQBIOlhtKM1PTHt+tbwwmQvrWGezu4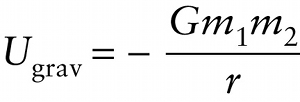
Review
The expression in Equation 10-4 looks nothing like the familiar formula \(U_{\mathrm{grav}} = mgy\). To understand the difference, let’s consider two different cases in which gravitational potential energy changes (Figure 10-8).
In Figure 10-8a a woman on Earth’s surface raises a book of mass \(m_{\mathrm{book}}\) a vertical distance \(d\). To do this she must work against a gravitational force on the book of magnitude \(m_{\mathrm{book}}g\), and so she must exert an upward force of the same magnitude. So she does an amount of work \(m_{\mathrm{book}}gd\) in the process. The book begins and ends at rest, so the work \(m_{\mathrm{book}}gd\) that she does goes into increasing the gravitational potential energy associated with the book: \(\Delta{U_{\mathrm{grav}}} = m_{\mathrm{book}}gd\). If the woman stands on a ladder and once again lifts the book by a distance \(d\), the gravitational force she works against is still \(m_{\mathrm{book}}g\) since the gravitational force exerted by Earth changes hardly at all near Earth’s surface. So she again does work \(m_{\mathrm{book}}gd\), and the gravitational potential energy increases by the same amount \(m_{\mathrm{book}}gd\) as before. As Figure 10-8b shows, this means that the gravitational potential energy increases in direct proportion to the object’s height \(y\), and so the graph of \(U_{\mathrm{grav}}\) versus height is a straight line: \(U_{\mathrm{grav}} = m_{\mathrm{book}}gy\).
Now imagine the same person has donned a spacesuit and has brought the book with her to a point in space a distance \(r_A\) from the center of Earth (Figure 10-8c). At this point the gravitational force that Earth exerts on the book has magnitude \(F_A = Gm_{\mathrm{Earth}}m_{\mathrm{book}}/r_A^2\). If she moves the book an additional distance \(d\) away from Earth, she has to exert a force of the same magnitude on the book and so does an amount of work \(F_{A}d = (Gm_{\mathrm{book}}/r_A^2)d\). Just as on Earth, the work that she does goes into increasing the gravitational potential energy. If she now moves to a greater distance \(r_B\) from the center of Earth and repeats the process, Earth's gravitational force has a smaller magnitude \(F_B = Gm_{\mathrm{Earth}}m_{\mathrm{book}}/r_B^2\)d, and so adds a smaller amount of gravitational potential energy. This means that at great distances, the gravitational potential energy does \(\textit{not}\) increase in direct proportion to the distance \(r\) and the graph of \(U_{\mathrm{grav}}\) versus distance is not a straight line. Instead, the graph becomes shallower with increasing values of \(r\) (Figure 10-8d). This is just what Equation 10-4 tells us, which helps to justify this expression for gravitational potential energy.