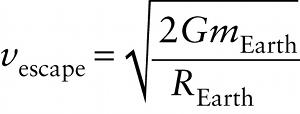Escape speed (10-10)
Question 1 of 4
Question
Speed that a projectile must have at Earth’s surface in order to escape Earth.
{"title":"Speed that a projectile must have at Earth’s surface in order to escape Earth.","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"1,48,20,69\"}]"} {"title":"Gravitational constant","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"181,14,208,44\"}]"} {"title":"Mass of Earth","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"poly\",\"coords\":\"113,132\"},{\"shape\":\"rect\",\"coords\":\"210,20,238,45\"}]"} {"title":"Radius of Earth","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"170,69,197,99\"}]"}Review
The initial speed \(v_i\) for which Equation 10-9 is true is called the escape speed, which we denote by the symbol \(v_{\mathrm{escape}}\) . This is the minimum speed at which an object must be launched from Earth’s surface to escape to infinity. To find its value, replace \(v_i\) in Equation 10-9 with \(v_{\mathrm{escape}}\), add \(Gm_{\mathrm{Earth}}m/R_{\mathrm{Earth}}\) to both sides and multiply both sides by \(2/m\).
\(\frac{1}{2}mv_{\mathrm{escape}}^2 = \frac{Gm_{\mathrm{Earth}}m}{R_{\mathrm{Earth}}}\)
\(v_{\mathrm{escape}}^2 = \frac{2Gm_{\mathrm{Earth}}}{R_{\mathrm{Earth}}}\)
Finally, take the square root of both sides: