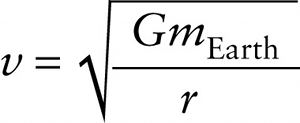Speed of an Earth satellite in a circular orbit (10-11)

Question 1 of 4

Question

Speed of an Earth satellite in a circular orbit

{"title":"Speed of an Earth satellite in a circular orbit","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"1,48,22,77\"}]"} {"title":"Gravitational constant","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"131,9,166,47\"}]"} {"title":"Mass of Earth","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"poly\",\"coords\":\"113,132\"},{\"shape\":\"rect\",\"coords\":\"195,33,199,34\"},{\"shape\":\"rect\",\"coords\":\"167,23,211,47\"}]"} {"title":"Radius of the satellite's orbit","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"175,84,202,114\"}]"}

Review

We can find the speed $v$ required for a circular orbit of radius $r$ from Equation 3-17 for the acceleration in uniform circular motion $a_{\mathrm{cent}} = v^2/r$ . For a satelite of mass $m$ orbiting Earth, the acceleration is provided by Earth's gravitational force. From Newton's second law, this says

$F_{\mathrm{Earth\ on\ satelite}} = ma_{\mathrm{cent}}$

or from Equation 3-17 for uniform circular motion and Equation 10-2 for the law of universal gravitation,

$\frac{Gm_{\mathrm{Earth}}m}{r^2} = m\frac{v^2}{r}$

To solve for $v$ , multiply both sides of this equation by $r/m$

$\frac{Gm_{\mathrm{Earth}}}{r} = v^2$

and take the square root: