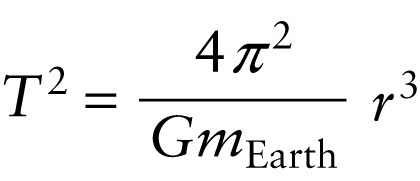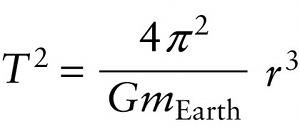Relationship between orbital period and radius for a circular orbit (10-12)

Question 1 of 4

Question

Mass of Earth

{"title":"Period of an Earth satellite in a circular orbit","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"1,48,28,82\"}]"} {"title":"Radius of the satellite's orbit","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"118,11,119,13\"},{\"shape\":\"rect\",\"coords\":\"264,59,285,90\"}]"} {"title":"Mass of Earth","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"poly\",\"coords\":\"113,132\"},{\"shape\":\"rect\",\"coords\":\"195,33,199,34\"},{\"shape\":\"rect\",\"coords\":\"139,91,177,115\"}]"} {"title":"Gravitational constant","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"109,82,136,112\"}]"}

Review

Another useful way to describe how rapidly a satellite moves around its circular orbit is in terms of the $\textbf{orbital period}$ , which is the time required to complete one orbit. In uniform circular motion the speed $v$ is constant, so the orbital period $T$ is just the circumference $2\pi{r}$ of the orbit (the distance around the circular orbit of radius $r$ ) divided by the speed: $T = 2\pi{r}/v$ . Using Equation 10-11 for $v$ , this becomes

$T = \frac{2\pi{r}}{v} =2\pi{r}\sqrt{\frac{r}{Gm_{\mathrm{Earth}}}}$

It's convenient to square both sides of this equation so as to eliminate the square root. Note that the square of $r$ is $r^2$ and the square of $\sqrt{r}$ is $r$ , so we end up with a factor of $r^2 \times r = r^3$ on the right-hand side of the equation: