Chapter 10. Newton's form of Kepler's law of periods (10-16)
Question
FV5Uk2WE5fUJF+tpUvZxTLkfpcjMu5ykVsSYedkkYc+eT6ye7+ewtWGj/i5zD1DemGiwvXcWfhSssHapJt0V7Q==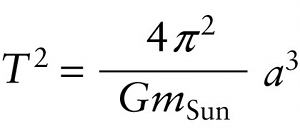
Question
8SiXQXN1NR0MfEE2Zq7kTgnxMiirxzLTL4TM+b9D6AEyNlHd6RjT0rJ32u8=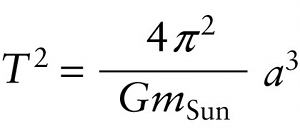
Question
4zx2+MEVfDjv0pcM+Aizi3VKNFQ=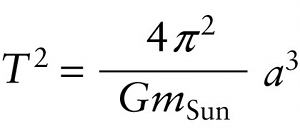
Question
2f0JqE4qJLZtiEw9M5xt/VAGtr3n12E9YgqnGA==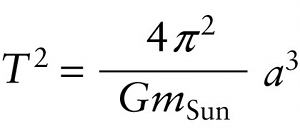
Review
The first two of Kepler’s laws describe how a given planet moves in its orbit. His third law, the \(\textbf{law of periods}\), compares the orbital periods of orbits of different sizes:
\(\textit{The square of the period of a planet’s orbit is proportional to the cube of the semimajor axis of the orbit.}\)
This is precisely the relationship that we found for circular orbits in Equation 10-12. Newton was able to show that the law of periods follows from the law of universal gravitation even for elliptical orbits, if we replace the orbital radius \(r\) in Equation 10-12 with the semimajor axis \(a\). For objects orbiting the Sun, we must also replace Earth’s mass \(m_{\mathrm{Earth}}\) with the mass of the Sun:
