Chapter 11. Net force on an object due to a pressure difference (11-10)
Question
PRkY3htaW/l/UpbvpMrfpf47AqAAR7z8gQN2kB79H74p8rD8/4vXIZ2JV0R1Xfc6fHA14SfieDjhhvo3x6GMJh2o7ytlyL79DNe+pHtBHzOSMtul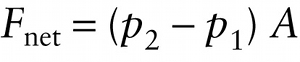
Question
ihL7q9kYqS2HIwJAz9K10T2P9wD9dIg2uS58RzoyKwWYsdyB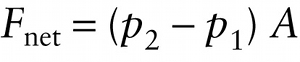
Question
c8v/wJ7B06y3Hygs/uFzwuPO6OUp2HU+uzUz5LsvNFlb6g10dstu4REOqmSdYNoBbRM7uNwLJRA=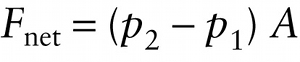
Question
ghPUVkki18HPTA+e/dRvdw80AzgVrQdOSZ1HPYn2yWw5r/W9OwUAjZqFQN8=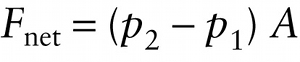
Review
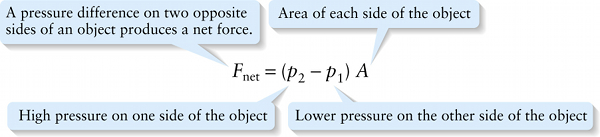
As a simple example of the force produced by a pressure difference, consider an object like a door with fluid on each side. The object has area \(A\), there is pressure \(p_1\) on one side of the object, and there is a greater pressure \(p_2\) on the \perpher side (Figure 11-10). By rearranging Equation 11-2, \(p = F_\perp /A\) we can calculate the magnitude of the force that each fluid exerts perpendicular to the object's surface:
Force on side 1: magnitude \(F_{\perp\ 1} = p_1A\)
Force on side 2: magnitude \(F_{\perp\ 2} = p_2A\)
Since \(p_2 >p_1\) the force \(F_{\perp\ 2}\) on side 2 is greater than the force \(F_{\perp\ 1}\) on side 1. These forces are in opposite directions, so the \(\textbf{net}\) force on the object has magnitude
\(F_{\mathrm{net}} = F_{\perp\ 2} - F_{\perp\ 1} = p_2A - p_1A\)
Equation 11-8 must be satisfied for a fluid to remain at rest, so this is also called the \(\textbf{equation of hydrostatic equilibrium}\).