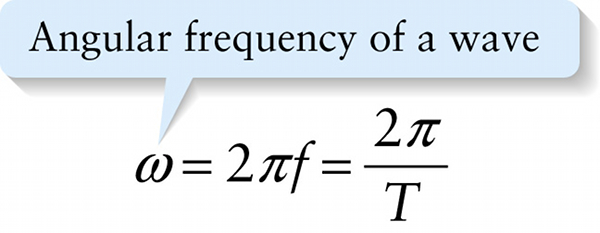Chapter 13. Angular frequency of a wave (13-1)

Review

To help us understand how a wave propagates over time, imagine a series of “snapshots” of a sinusoidal wave equally spaced in time like the frames of a movie. Figure 13-7 shows such a series. As the wave moves through the medium, an individual piece of the medium (like the blue dot in Figure 13-7) oscillates up and down. Just as in Section 12-2, we use the term period and the symbol \(T\) for the time required for each piece of the medium to go through a complete oscillation cycle. Furthermore, just as in Sections 12-2 and 12-3 the frequency \(f\) (in hertz, or Hz) is the number of cycles that a piece of the medium goes through per second, and the \(\textbf{angular frequency}\) \(\omega\) (in rads/s) equals the frequency multiplied by \(2\pi\):