Chapter 13. Speed of a longitudinal wave in a fluid (13-11)
Question
8AuWoBWpMMGf9bWZWMxFzwRYbeDa6XNtqKd1XigoiXqWdDO0SGZdDC1I4IoSYLbxyjd2xHeUArk=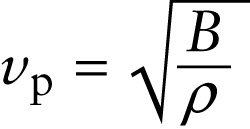
Question
yytoliRugU8RwJr1cJsNA/hUpx5qfyUtQvIxAwYj8aU=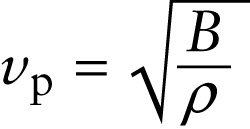
Question
tBsiNfUnwj/GaltJS6Frct4KgS6ns33w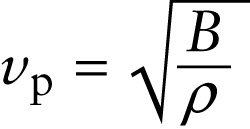
Review
Just as for a transverse wave on a rope, the speed of a \(\textit{longitudinal}\) wave in a medium depends on the restoring force and the inertia of the medium. For a longitudinal wave in a fluid (a gas or a liquid), we call a longitudinal wave a \(\textit{sound}\) wave. The disturbance associated with the wave corresponds to changes in the pressure of the fluid. We saw in Section 9-4 that the \(\textit{bulk modulus}\) \(B\) of a material is a measure of how it responds to pressure changes. A larger bulk modulus means the material is more difficult to compress, which means that it has a greater tendency to return to its original volume when the pressure is released. In \perpher words, the value of \(B\) tells us about the restoring force that acts within a fluid when disturbed by the pressure changes associated with a longitudinal wave. A measure of the inertia of the material is its density \(\rho\), equal to its mass per volume (see Example 13-3 above). A detailed analysis using Newton’s laws shows that the speed of sound waves in a fluid is
If we take both restoring force and inertia into account, we find that the propagation speed \(v_{\mathrm{p}}\) of a transverse wave on a rope is
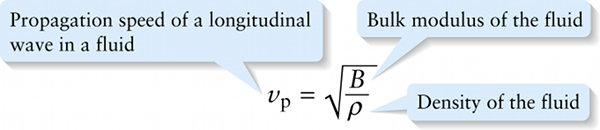
The greater the bulk modulus \(B\), the faster the propagation speed; the greater the density \(\rho\), the slower the propagation speed.