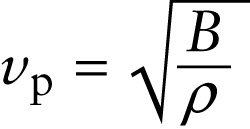Speed of a longitudinal wave in a solid rod (13-12)

Balloon Art Concept Check: Click on the part of the equation that is described by the bubble text shown

Question 1 of 3

Question

Propagation speed of a longitudinal wave along a solid rod
Feedback
{"title":"Propagation speed of a longitudinal wave along a solid rod","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"3,51,28,85\"}]"} {"title":"Young’s modulus of the solid","description":"Wrong","type":"incorrect","color":"#993300","code":"[{\"shape\":\"rect\",\"coords\":\"187,9,226,57\"}]"} {"title":"Density of the solid ","description":"Wrong","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"180,79,219,128\"}]"}

Review

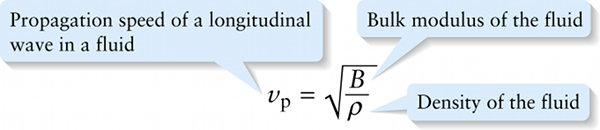
The speed of longitudinal waves in a \(\textit{solid}\) is given by a different expression than Equation 13-11. If we just consider one-dimensional waves such as those that might travel the length of a solid rod, what matters is not the \(\textit{bulk}\) modulus \(B\) but rather \(\textit{Young’s modulus}\) \(Y\). We learned in Section 9-2 that Young’s modulus tells us how difficult it is to stretch or compress a piece of material along its length; those are just the kind of stresses experienced in a rod with a longitudinal wave propagating down its long axis. So \(Y\) tells us about the restoring force in this case, and the propagation speed is