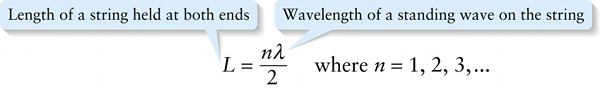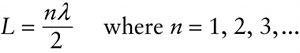Chapter 13. Wavelengths for a standing wave on a string (13-18)

Question

+v3V7Kx4VIxXs+fD4evpLuZSZ4cQGaef2StgYNC7nwx6oR46hFKzaQ==

{"title":"Length of a string held at both ends","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"1,12,16,36\"}]"} {"title":"Wavelength of a standing wave on the string","description":"Wrong","type":"incorrect","color":"#993300","code":"[{\"shape\":\"rect\",\"coords\":\"58,5,71,21\"}]"}

Question

N1iUHjn3DZOl/ASwewjUN3J88RZHL24d5AihecJITJyEg6KEjhVvz/rt+Ot7W9TR

{"title":"Length of a string held at both ends","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"1,12,16,36\"}]"} {"title":"Wavelength of a standing wave on the string","description":"Correct!","type":"correct","color":"#993300","code":"[{\"shape\":\"rect\",\"coords\":\"58,4,71,22\"}]"}

Review

Here \(\lambda\) represents the wavelength of both the standing wave and also the original wave we created on the string. So according to Equation 13-18, a whole number \(n\) of half-wavelengths must fit onto the string to generate the standing wave pattern described by Equation 13-16. Figure 13-14 shows the patterns for \(n = 1\) (for which half of a wavelength fits), \(n = 2\) (for which two half-wavelengths, or one full wavelength, fits), and \(n = 3\) (for which three half-wavelengths, or one and a half full wavelengths, fits). Each of these patterns is called a \(\textbf{standing wave mode}\).