Frequencies for a standing wave on a string (13-19)

Balloon Art Concept Check: Click on the part of the equation that is described by the bubble text shown

Question 1 of 4

Question

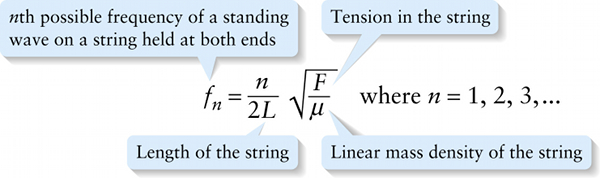
\(n\)th possible frequency of a standing wave on a string held at both ends
Feedback
{"title":"nth possible frequency of a standing wave on a string held at both ends","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"1,12,16,36\"}]"} {"title":"Tension in the string","description":"Wrong","type":"incorrect","color":"#993300","code":"[{\"shape\":\"rect\",\"coords\":\"90,3,107,19\"}]"} {"title":"Linear mass density of the string","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"90,29,103,43\"}]"} {"title":"Length of the string","description":"Wrong","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"48,26,64,42\"}]"}

Review

By combining Equations 13-2 and 13-10, we get the following relationship between the frequency \(f\) and wavelength \(\lambda\) of a wave on a string:

\(f\lambda = \sqrt{\frac{F}{\mu}}\) or \(f = \frac{1}{\lambda}\sqrt{\frac{F}{\mu}}\)

To make this specific to \(\textit{standing}\) waves on a string, we use the relation \(L = n\lambda/2\) from Equation 13-18, which we can rewrite as \((1\ /\ \lambda) = n\ /\ (2L)\). Substituting this into the above equation, we get: