Chapter 13. Wavelengths for a standing sound wave in an open pipe (13-23)

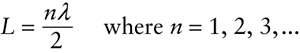
Review

Because this pipe is open at each end, there is a displacement antinode (pressure node) at each end. Figure 13-20 shows the displacement patterns for the first three standing wave modes of such a pipe. (Just as at the open end of a closed pipe, a sound wave traveling through an open pipe is partially reflected at each open end. The traveling waves moving in opposite directions through the pipe give rise to a standing wave.) You can see that in Figure 13-20a one half-wavelength fits in the length \(L\) of the pipe. This represents the fundamental mode of the pipe, so the wavelength \(\lambda\) of the fundamental mode is given by

\(L = \frac{1}{2}\lambda\)

Similarly, the standing wave modes in Figures 13-20b and 13-20c have two half-wavelengths (one full wavelength) and three half-wavelengths, respectively, in the length of the pipe. In general, the relationship between \(L\) and \(\lambda\) for an open pipe is