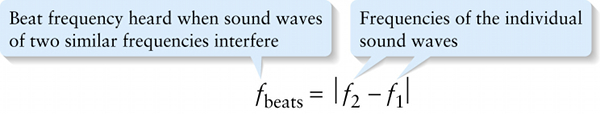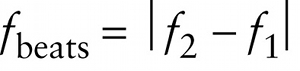Beat frequency (13-25)

Question 1 of 2

Question

Frequencies of the individual sound waves

{"title":"Beat frequency heard when sound waves of two similar frequencies interfere","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"1,7,23,59\"}]"} {"title":"Frequencies of the individual sound waves","description":"Correct!","type":"correct","color":"#993300","code":"[{\"shape\":\"rect\",\"coords\":\"159,8,186,56\"},{\"shape\":\"rect\",\"coords\":\"240,7,270,59\"}]"}

Review

To see how beats arise, let’s see what happens when we combine two sinusoidal waves with the same amplitude A but with slightly different frequencies $f_1$ and $f_2$ . Figure 13-21 shows the result: The total wave is also a sinusoidal wave whose frequency $f$ is the average of $f_1$ and $f_2$ , but with an amplitude that varies between 0 and $2A$ . We use the term beats for this up-and-down variation in amplitude. The frequency of the beats, also called the $\textbf{beat frequency}$ , is equal to the $\textit{absolute value}$ of the difference between the two frequencies: