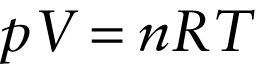Ideal gas law in terms of number of moles (14-7)
Question
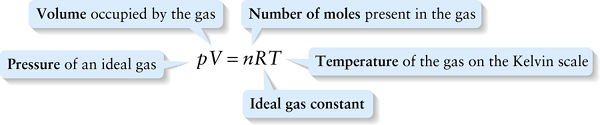
\(\textbf{Temperature}\) of the gas on the Kelvin scale
{"title":"Volume occupied by the gas","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"38,8,77,51\"}]"} {"title":"Number of moles present in the gas","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"138,22,168,53\"}]"} {"title":"Temperature of the gas on the Kelvin scale","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"215,3,259,52\"}]"} {"title":"Ideal gas constant","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"172,5,211,54\"}]"} {"title":"Pressure of an ideal gas","description":"Wrong","type":"incorrect","color":"#333333","code":"[{\"shape\":\"rect\",\"coords\":\"1,13,31,65\"}]"}Review
Given the very large number of molecules in most samples of gas, it’s often more convenient to write Equation 14-6 in terms of the number of \(\textit{moles}\) of a gas. One \(\textbf{mole}\) of a substance contains as many molecules as there are atoms in exactly 12 grams of carbon-12, the variety of carbon that has six protons and six neutrons in its nucleus. To four significant figures the mole, abbreviated mol, contains \(6.022 \times 10^{23}\) molecules. This value is called Avogadro’s number \(N_{\mathrm{A}}\):
\(N_A = 6.022 \times 10^{23}\) molecules/mol
The number \(N\) of molecules in a substance is therefore equal to the number of moles \(n\) multiplied by Avogadro's number: \(N = nN_A\). Then Equation 14-6 becomes
\(pV = nN_AkT\)
The product of \(N_Ak\) has a special name: We call it the \(\textbf{ideal gas constant}\) and give it the symbol \(R\). To four significant figures,
\(R = N_{A}k = 8.314\mathrm{J} / (\mathrm{mol} \cdot \mathrm{K})\)
With this definition, the ideal gas law (Equation 14-6 becomes