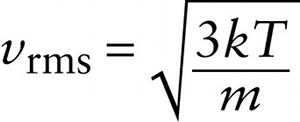Root-mean-square speed of molecules in an ideal gas (14-15)
Question
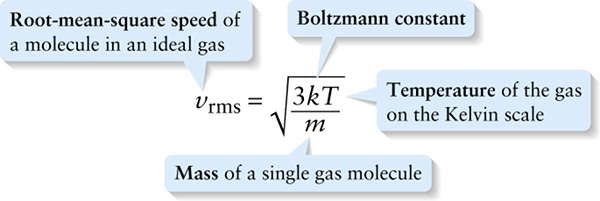
\(\textbf{Root-mean-square speed}\) of a molecule in an ideal gas
{"title":"Root-mean-square speed of a molecule in an ideal gas","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"1,34,90,78\"}]"} {"title":"Boltzmann constant","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"225,16,250,59\"}]"} {"title":"Temperature of the gas on the Kelvin scale","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"253,16,288,59\"}]"} {"title":"Mass of a single gas molecule","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"222,83,260,114\"}]"}Review
A measure of how fast gas molecules move on average is the \(\textbf{root-mean-square speed}\) or \(\textbf{rms speed}\). To see how this is defined, first imagine finding the average value of \(v^2\), the square of the speed \(v\), for all the molecules in a gas that have a given mass \(m\). This is the quantity that we’ve called \((v^2)_{\mathrm{average}}\). Another word for average is mean, which is why \((v^2)_{\mathrm{average}}\) is called the mean-square of the speed. The root-mean-square speed is the square root of the mean-square:
\(v_{\mathrm{rms}} = \sqrt{(v^2)_{\mathrm{average}}}\)
Note that \((v^2)_{\mathrm{average}}\) has units of m/s. From Equation 14-13, \((1/2)m(v^2)_{\mathrm{average}} = (3/2)kT\), so \((v^2)_{\mathrm{average}} = 3kT/m\). If we substitute this into Equation 14-14 we get: