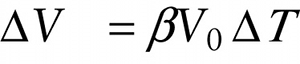Change in volume due to a temperature change (14-19)

Question 1 of 4

Question

Temperature change of the substance that causes the volume

{"title":"Change in the volume of a quantity of substance","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"2,4,68,45\"}]"} {"title":"Volume of the substance before the temperature change","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"181,8,209,45\"}]"} {"title":"Temperature change of the substance that causes the volume change","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"233,3,301,52\"}]"} {"title":"Coefficient of volume expansion of the substance","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"142,4,178,56\"}]"}

Review

When the temperature of a solid object changes, its length, width, and height change according to the linear thermal expansion relationship of Equation 14-18. As a result, its volume expands as well. A fluid (a liquid or gas) has no fixed dimensions, however, so Equation 14-18 doesn’t apply, but fluids also change their volume when the temperature changes. An equation that describes the volume change with temperature for solids and fluids alike is

The coefficient of volume expansion $\beta$ (Greek letter beta) also has units of $\mathrm{K}^{-1}$ or $(^{\circ}\mathrm{C})^{-1}$ .