Chapter 14. Quantity of heat and the resulting temperature change (14-20)
Question
UrmwavQtUzuwHVlhZYkVmBfV/yvm7DJxYZsvfZ39BIMPezBMgjmGpMdmdRPmbYRifdknJYMQgO1uYoKSUkFpgPucXbO1YWX5INnyIpw9QrS3HGApMIPcV586cYM=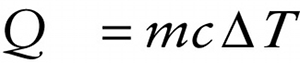
Question
Qu0mSrPCc5T3a8jLmTwUjwbzqob8QNbdPDsLxoEEHytnS8rRzZtrKU7PZYGW+GD+Wzxyju74lxXViY6e3kGWFQ==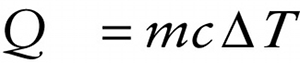
Question
I0C0x48r0aDjpm99mTxAsvB2sHMVpl1yGEMbyoDdErqGod6CSbA89uE2uBRI62wN4Ocq8fnBeuCH0kbTLZMbWG9581I=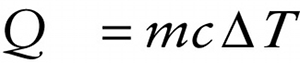
Question
Btgotq5ANHx8Ew2TXWow2anVxsJBjJbH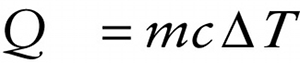
Review
Experiment shows that in most circumstances the flow of heat into or out of an object changes the object’s temperature. (The exception is when the object undergoes a phase change such as from solid to liquid, liquid to solid, liquid to gas, or gas to liquid. In the next section we’ll discuss what happens in a phase change.) If the quantity of heat \(Q\) that flows into an object is rela tively small, the resulting temperature change \(\Delta{T}\) turns out to be directly proportional to \(Q\) and inversely proportional to the mass \(m\) of the object. In other words, the greater the quantity of heat \(Q\) that flows into an object, the more its temperature changes; the more massive the object and so the more material that makes up the object, the smaller the temperature change for a given quantity of heat \(Q\). (The same quantity of heat that will cook a single meatball will cause hardly any temperature change in a pot roast.) We can write this relationship as
\(\Delta{T} = (\mathrm{constant}) \times \frac{\mathrm{Q}}{m}\)
The constant in this equation depends on the substance of which the object is made. It’s conventional to express this equation as
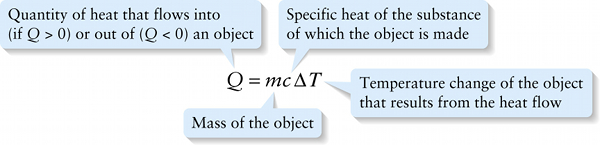
The quantity \(c\) is called the specific heat of the material that makes up the object. Its units are joules per kilogram per Kelvin (\(\mathrm{J}/(\mathrm{kg}\cdot\mathrm{K)}\) or \(\mathrm{J} \cdot \mathrm{kg}^{-1} \cdot \mathrm{K}^{-1})\) For example, the value of \(c\) for aluminum is 910 \(\mathrm{J}/(\mathrm{kg} \cdot \mathrm{K})\); this means that 910 J of heat must flow into a 1-kg block of aluminum to raise its temperature by 1 K (or, equivalently, \(1^\circ\mathrm{C}\)).