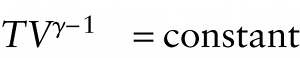Temperature and volume for ideal gas, adiabatic process (15-23)

Balloon Art Concept Check: Click on the part of the equation that is described by the bubble text shown

Question 1 of 4

Question

Kelvin temperature of an ideal gas
Feedback
{"title":"Kelvin temperature of an ideal gas","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"2,15,25,49\"}]"} {"title":"Volume of an ideal gas","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"32,15,52,50\"}]"} {"title":"Ratio of specific heats of the gas = Cp /CV","description":"Wrong","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"53,20,67,39\"}]"} {"title":"The quantity TVγ −1 has the same value at all times during an adiabatic process for an ideal gas.","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"163,27,298,49\"}]"}

Review

The value of g is greater than 1 for all gases (see Table 15-1), so \(\gamma - 1\) is greater than zero. So as volume increases in an adiabatic expansion, temperature decreases; as volume decreases in an adiabatic compression, temperature increases.

Equation 15-23 explains what happens when you use a bicycle pump to inflate a tire: The pump rapidly becomes warm to the touch. Although the pump is not made of an insulating material, the air in the pump cylinder is compressed so rapidly that there’s no time for heat to flow into or out of the air during the compression. As a result the compression is adiabatic, so the temperature of the gas (and the pump that holds it) increases as the air is compressed.