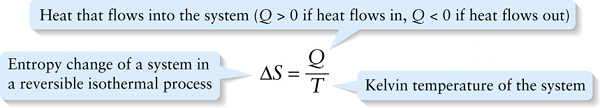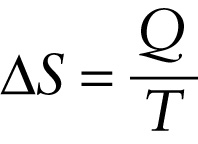Entropy change in a reversible isothermal process (15-33)

Balloon Art Concept Check: Click on the part of the equation that is described by the bubble text shown

Question 1 of 3

Question

Entropy change of a system in a reversible isothermal process
Feedback
{"title":"Entropy change of a system in a reversible isothermal process","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"33,50,69,99\"}]"} {"title":"Heat that flows into the system (Q > 0 if heat flows in, Q < 0 if heat flows out)","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"137,4,194,64\"}]"} {"title":"Kelvin temperature of the system","description":"Wrong","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"142,86,188,133\"}]"}

Review

The entropy change \(\Delta{S}\) in an isothermal expansion also depends on the temperature \(T\). For a given quantity of heat \(Q\), the increase in disorder is greater if the system is at a low temperature (so the molecules are moving slowly and are relatively well ordered to start with) than if the system is at a high temperature (so the molecules are moving rapidly in a relatively disordered state). We conclude that the entropy change \(\Delta{S}\) in this reversible isothermal process is inversely proportional to the Kelvin temperature \(T\).

Putting these ideas together, we define the entropy change \(\Delta{S}\) in a reversible isothermal process as