Chapter 16. Electric field and electric force (16-2)
Question
nCc/JQxnlNPUpcfdq7Su8MdCEziUQpbkrDJ4yEaaDB90hFqo7xcJ034qjIFMW9NrXYMR9n1vAo3gaCT5JzyqUWEVdufE+8k9GUkdGVCF1b4aGMkjXTyBnTmlIEFsjZ4gFkK+uUzZ5dH75ICioP5hrKZl069C2KdGVenj2Q==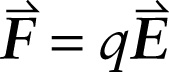
Question
5TjszOmok3C3Ogo/5s7I+H7+nxLlHurUk6jhkE+fVTyxm7pXgW4xNISdqCMTyyKMR/v2iDG8mTQxlvC/cwiuNsDBpN7Ytu/8OJDKKQ==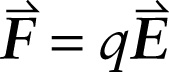
Review
Most forces in our daily experience arise only when one object is in direct contact with another object. Two examples are the normal force that acts on your body when you sit in a chair or when you push directly on an object. Nevertheless, some forces, such as the gravitational force and the Coulomb force, appear to act even between two objects separated by a distance. The fundamental theory of interactions between particles suggests that objects exert forces on each other by exchanging small units of energy or matter. For our purposes, however, a more useful approach employs the concept of the field. In this view, every charged object modifies all of space by producing an electric field, which is strongest closest to the object but extends infinitely far away. A second charged object senses this change in space, interacting with the electric field and experiencing an electric force (Figure 16-8).
If we place a particle carrying charge \(q\) in an electric field \(\vec{E}\), the force experienced by the particle is
