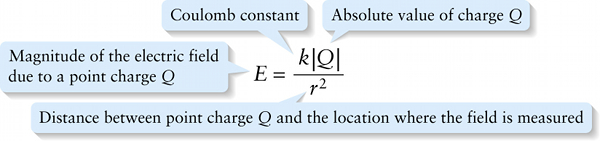
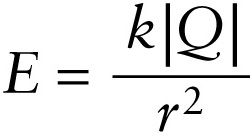Magnitude of the electric field due to a point charge (16-4)

Question 1 of 4

Question

Magnitude of the electric field due to a point charge $Q$

{"title":"Magnitude of the electric field due to a point charge Q","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"5,50,40,94\"}]"} {"title":"Coulomb constant","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"125,2,160,49\"}]"} {"title":"Absolute value of charge Q","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"175,3,225,64\"}]"} {"title":"Distance between point charge Q and the location where the field is measured","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"153,98,183,135\"}]"}

Question

Absolute value of charge $Q$

{"title":"Magnitude of the electric field due to a point charge Q","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"5,50,40,94\"}]"} {"title":"Coulomb constant","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"125,2,160,49\"}]"} {"title":"Absolute value of charge Q","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"175,3,225,64\"}]"} {"title":"Distance between point charge Q and the location where the field is measured","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"153,98,183,135\"}]"}

Question

Distance between point charge $Q$ and the location where the field is measured

{"title":"Magnitude of the electric field due to a point charge Q","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"5,50,40,94\"}]"} {"title":"Coulomb constant","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"125,2,160,49\"}]"} {"title":"Absolute value of charge Q","description":"Wrong","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"175,3,225,64\"}]"} {"title":"Distance between point charge Q and the location where the field is measured","description":"Correct!","type":"correct","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"153,98,183,135\"}]"}

Review

We can use Coulomb’s law, Equation 16-1, to write an expression for the magnitude of the electric field due to a point charge $Q$ . If we place a test charge $q$ a distance $r$ from charge $Q$ , Equation 16-1 tells us that the magnitude of the Coulomb force on $q$ is $F = k\left|q\right|\left|Q\right|r^2$ . From Equation 16-2, we can also write this force magnitude as $F = \left|q\right|E$ , where $E$ is the magnitude of the electric field due to charge $Q$ at the position of test charge $q$ . Setting these two expressions for $F$ equal to each other, we get

$\left|q\right|E = \frac{k\left|q\right|\left|Q\right|}{r^2}$